已知：平面α∩平面β=l，α⊥平面γ，β⊥平面γ．
求证：l⊥γ．
(本小题满分12分)已知定义域为
的函数
满足
.
（1）若
,求
；又若
,求
；
（2）设有且仅有一个实数
,使得
,求函数的解析表达式.
（本小题满分12分）已知椭圆
的方程为
，双曲线
的左、右焦
点分别是的左、右顶点，而的左、右顶点分别是的左、右焦点.
（1）求双曲线的方程；
（2）若直线
与双曲线C2恒有两个不同的交点A和B，求
的范围。
（本小题满分12分）设
为等差数列, {bn}为等比数列, 且a1=b1=1,a2+a4=b3, b2b4=a3，分别求出{an}与{bn}的通项公式.
（本小题满分12分）已知
中∠ACB=90°，AS=BC=1，AC=2，SA⊥面ABC，AD⊥SC于D，
（1）求证： AD⊥面SBC；
（2）求二面角A-SB-C的大小.
(本小题满分12分)甲、乙、丙三人在同一办公室工作，办公室里有一部电话机，设经该机打进的电话打给甲、乙、丙的概率依次为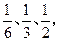
若在一段时间内打进三个电话，
且各个电话相互独立，求：
（1）这三个电话是打给同一个人的概率；
（2）这三个电话中恰有两个是打给同一个人的概率.