(本小题满分12分)已知定义域为 的函数
的函数 满足
满足 .
.
(1)若 ,求
,求 ;又若
;又若 ,求
,求 ;
;
(2)设有且仅有一个实数 ,使得
,使得 ,求函数
,求函数 的解析表达式.
的解析表达式.
在△ABC中,a、b、c分别是角A、B、C的对边,且 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若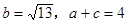 ,求△ABC的面积.
,求△ABC的面积.
己知函数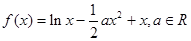
(1)若 ,求函数
,求函数 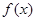 的单调递减区间;
的单调递减区间;
(2)若关于x的不等式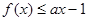 恒成立,求整数 a的最小值:
恒成立,求整数 a的最小值:
(3)若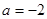 ,正实数
,正实数 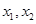 满足
满足 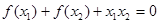 ,证明:
,证明: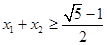
已知函数 ,函数
,函数 .
.
(1)当 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值;
(2)当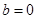 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数 的图象的公共点的个数;
的图象的公共点的个数;
(3)函数 的图象能否恒在函数
的图象能否恒在函数 的图象的上方?若能,求出
的图象的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数 ,
,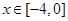 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.
(1)试确定A, 和
和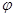 的值;
的值;
(2)现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
已知函数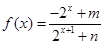 ,(其中
,(其中 、
、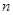 为参数)
为参数)
(1)当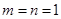 时,证明:
时,证明: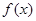 不是奇函数;
不是奇函数;
(2)如果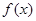 是奇函数,求实数
是奇函数,求实数 、
、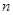 的值;
的值;
(3)已知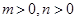 ,在(2)的条件下,求不等式
,在(2)的条件下,求不等式 的解集.
的解集.