平面内动点P(x，y)与两定点A(-2, 0), B(2,0)连线的斜率之积等于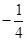
，若点P的轨迹为曲线E，过点 
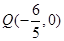直线 
交曲线E于M，N两点．
（Ⅰ）求曲线E的方程，并证明：
MAN是一定值；
（Ⅱ）若四边形AMBN的面积为S，求S的最大值
（本小题满分13分）已知△ABC的周长为6，
成等比数列，求
（1）△ABC的面积S的最大值；
（2）
的取值范围。
已知
，其中0< 
<2,
(1) 解不等式。（2）若x>1时，不等式恒成立,求实数m的范围。
(本题满分13分)已知数列{an}的前n项和为Sn，且an=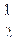
(3n+Sn)对一切正整数n成立
（I）证明：数列{3+an}是等比数列，并求出数列{an}的通项公式；
（II）设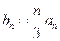
，求数列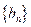
的前n项和Bn；
如图，要计算西湖岸边两景点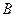
与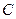
的距离，由于地形的限制，需要在岸上选取
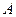和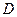
两点，现测得
，
，
，
，
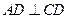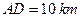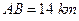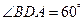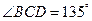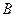，求两景点与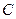的距离（精确到0.1km）．参考数据：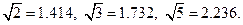
已知数列{an}满足2an+1=an+an+2 (n∈N*),它的前n项和为Sn，且a3=-6,S6=-30.求数列{an}的前n项和的最小值.