(本题满分13分)已知数列{an}的前n项和为Sn,且an=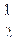 (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设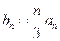 ,求数列
,求数列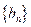 的前n项和Bn;
的前n项和Bn;
)已知数列{an}是首项为-1,公差d  0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
(1)求{an}的通项公式;
(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
己知函数f(x)=ex,x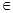 R.
R.
(1)若直线y=kx+1与f(x)的反函数图象相切,求实数k的值;
(2)设x﹥0,讨论曲线y=f(x)与曲线y=mx2(m﹥0)公共点的个数;
(3)设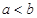 ,比较
,比较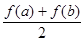 与
与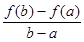 的大小并说明理由。
的大小并说明理由。
已知函数f(x)=x3+ax-2,(a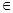 R).
R).
(l)若f(x)在区间(1,+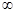 )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;
(2)若 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;
(3)若 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。
如图,正三棱柱ABC-A'B'C'中,D是BC的中点,AA'=AB=2.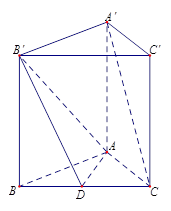
(1)求证:A'C//平面AB'D;
(2)求二面角D一AB'一B的余弦值。
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图。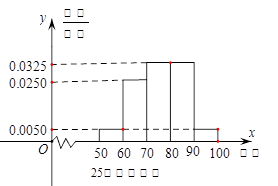
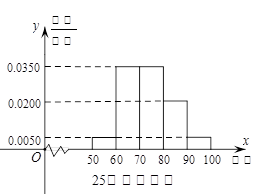
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。