某工厂有25周岁以上(含2S周岁)工人300名，25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计，得到如图所示的频率分布直方图。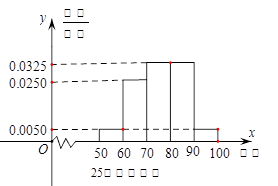
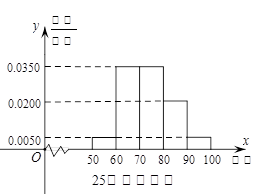
(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数；
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”；“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人，求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件，“菜鸟”日平均生产件数视为55件)。
已知条件
，条件
，若
是
的充分条件，求实数
的取值范围．
已知函数
．
（1）求函数
的单调区间；
（2）当
时，
，求实数
的取值范围．
己知椭圆C：
（a＞b＞0）的右焦点为F（1，0），点A（2，0）在椭圆C上，过F点的直线
与椭圆C交于不同两点
．
（1）求椭圆C的方程；
（2）设直线斜率为1，求线段
的长；
（3）设线段的垂直平分线交
轴于点P（0，y0），求的取值范围．
2015年某市某区高考文科数学成绩抽样统计如下表：
（1）求出表中m、n、M、N的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图；（纵坐标保留了小数点后四位小数）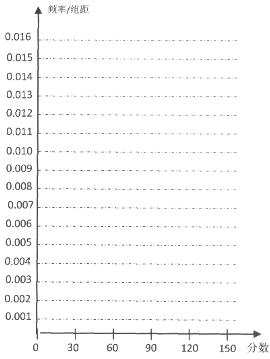
（2）若2015年某市高考文科考生共有20000人，试估计全市文科数学成绩在90分及90分以上的人数；
（3）香港某大学对内地进行自主招生，在参加面试的学生中，有7名学生数学成绩在140分以上，其中男生有4名，要从7名学生中录取2名学生，求其中恰有1名女生被录取的概率．
已知椭圆
：
，直线
交椭圆于
两点．
（Ⅰ）求椭圆的焦点坐标及长轴长；
（Ⅱ）求以线段
为直径的圆的方程．