己知椭圆C：
（a＞b＞0）的右焦点为F（1，0），点A（2，0）在椭圆C上，过F点的直线
与椭圆C交于不同两点
．
（1）求椭圆C的方程；
（2）设直线斜率为1，求线段
的长；
（3）设线段的垂直平分线交
轴于点P（0，y0），求的取值范围．
已知向量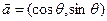
，向量
，求
的最大值和最小值。
甲，乙两人进行乒兵球比赛，在每一局比赛中，甲获胜的概率为
。
(1)如果甲，乙两人共比赛4局，甲恰好负2局的概率不大于其恰好胜3局的概率，试求的取值范围；
(2)若
，当采用3局2胜制的比赛规则时，求甲获胜的概率；
(3)如果甲，乙两人比赛6局，那么甲恰好胜3局的概率可能是
吗？
袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不返回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量
为此时已摸球的次数，求：
(1)随机变量的概率分布列；(2)随机变量的数学期望与方差.
有六节电池，其中有2只没电，4只有电，每次随机抽取一个测试，不放回，直至分清楚有电没电为止，所要测试的次数
为随机变量，求的分布列.
在10件产品中有2件次品，连续抽3次，每次抽1件，求：
（1）不放回抽样时，抽到次品数
的分布列；
（2）放回抽样时，抽到次品数
的分布列.