一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
盒中装有16个球,其中6个是玻璃球,10个是木质球.玻璃球中有2个是红色的,4个是蓝色的;木质球中有3个是红色的,7个是蓝色的.
(1)现从中任取1个,已知取到的是蓝球,问该球是玻璃球的概率是多少?
(2)现从中任取1个,取后放回,则第一次取到的是蓝球且第二次取得的是玻璃球的概率是多少?
某校举行运动会,组委会招墓了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下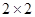 列联表:
列联表: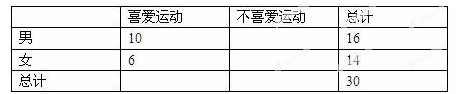
(2)根据列联表的独立性检验,有多大的把握认为性别与喜爱运动有关?
(3)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率。
参考公式: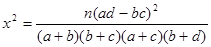 (其中
(其中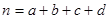 )
)
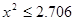 |
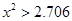 |
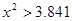 |
 |
|
| 是否有关联 |
没有关联 |
90% |
95% |
99% |
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
已知函数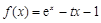 (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数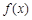 的单调增区间;
的单调增区间;
(2)设不等式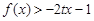 的解集为M,且集合
的解集为M,且集合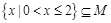 ,求实数t的取值范围.
,求实数t的取值范围.
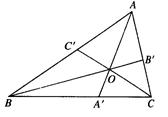
已知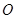 是
是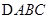 内任意一点,连结
内任意一点,连结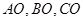 并延长交对边于
并延长交对边于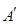 ,
,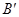 ,
,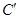 ,则
,则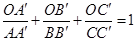 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”: 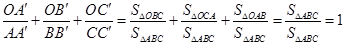 .
.
运用类比,猜想对于空间中的四面体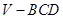 ,存在什么类似的结论,并用“体积法”证明。
,存在什么类似的结论,并用“体积法”证明。