△ABC中,角A、B、C对边分别是a、b、c,满足2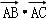 =a2﹣(b+c)2.
=a2﹣(b+c)2.
(Ⅰ)求角A的大小;
(Ⅱ)求2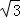 cos2
cos2 ﹣sin(
﹣sin(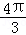 ﹣B)的最大值,并求取得最大值时角B、C的大小.
﹣B)的最大值,并求取得最大值时角B、C的大小.
(本小题满分12分)某中学选派 名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
名同学参加上海世博会青年志愿者服务队(简称“青志队”),他们参加活动的次数统计如表所示.
| 活动次数 |
 |
 |
 |
| 参加人数 |
 |
 |
 |
[
(Ⅰ)从“青志队”中任意选 名学生,求这
名学生,求这 名同学中至少有
名同学中至少有 名同学参加活动次数恰好相等的概率;
名同学参加活动次数恰好相等的概率;
(Ⅱ)从“青志队”中任选两名学生,用 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望 .
.
(本小题满分12分)设角 是
是 的三个内角,已知向量
的三个内角,已知向量 ,
, ,且
,且 .
.
(Ⅰ)求角 的大小; (Ⅱ)若向量
的大小; (Ⅱ)若向量 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分16分)设函数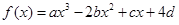 (
(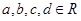 )的图象关于原点对称,且
)的图象关于原点对称,且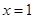 时,
时,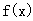 取极小值
取极小值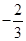 ,
,
①求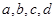 的值;
的值;
②当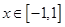 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
③若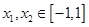 ,求证:
,求证: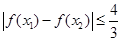 。
。
已知,数列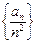
 是公比为
是公比为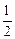 的等比数列,
的等比数列,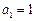 .
.
(1)求数列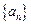 的通项公式;
的通项公式;
(2)令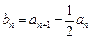 ,若数列
,若数列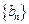 的前
的前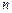 项和
项和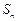 ,求证:
,求证: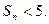
(本小题满分14分)
(理)已知数列{a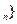 中,a
中,a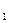 =5且a
=5且a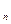 =3a
=3a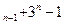 (n≥2)
(n≥2)
(1)求a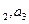 的值.
的值.
(2)设b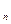 =
=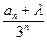 ,是否存在实数λ,使数列{b
,是否存在实数λ,使数列{b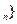 为等差数列,若存在请求其通项b
为等差数列,若存在请求其通项b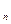 ,若不存在请说明理由.
,若不存在请说明理由.