设函数f(x)=x3﹣ x2﹣2x﹣
x2﹣2x﹣ .
.
(1)求函数f(x)的单调递增、递减区间;
(2)当x∈[﹣1,1]时,f(x)<m恒成立,求实数m的取值范围.
已知曲线C的参数方程为(α∈R,α为参数).当极坐标系的极点与直角坐标系的原点重合,且极轴 在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+)=a.
在x轴的正半轴上时,曲线D的极坐标力程为ρsin(θ+)=a.
(I)、试将曲线C的方程化为普通方程,曲线D的方程化为直角坐标方程;
(II)、试确定实数a的取值范围,使曲 线C与曲线D有公共点.
线C与曲线D有公共点.
已知a、b∈R,若M=\o(\s\up7(-1b所对应的变换TM把直线l:3x-2y=1变换为自身,试求实数a、b的值.
已知函数

(1)、若函数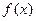 在
在 处的切线方程为
处的切线方程为 ,求
,求 的值;
的值;
(2)、若函数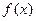 在
在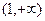 为增函数,求
为增函数,求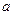 的取值范围;
的取值范围;
(3)、讨论方程
 解的个数,并说明理由。
解的个数,并说明理由。
已知数列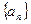 首项
首项 ,公比为
,公比为 的等比数列,又
的等比数列,又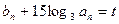 ,常数
,常数 ,数列
,数列 满足
满足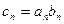 ,
,
(1)、求证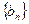 为等差数列;
为等差数列;
(2)、若 是递减数列,求
是递减数列,求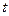 的最小值;(参考数据:
的最小值;(参考数据: )
)
(3)、是否存在正整数 ,使
,使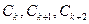 重新排列后成等比数列,若存在,求
重新排列后成等比数列,若存在,求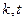 的值,若不存在,说明理由。
的值,若不存在,说明理由。
给定椭圆C: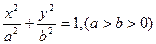 ,称圆心在原点O、半径为
,称圆心在原点O、半径为 的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为
的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 距离为
距离为 ;
;
(1)、求椭圆C的方程及其“伴椭圆”的方程;
(2)、若倾斜角为 的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
(3)、若点P是椭圆C“伴椭圆”上一动点,过点P作直线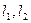 ,使得
,使得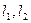 与椭圆C都只有一个公共点,求证:
与椭圆C都只有一个公共点,求证: 。
。