某中学对高二甲、乙两个同类班级进行加强语文阅读理解训练对提高数学应用题得分率作用的试验,其中甲班为实验班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用试题测试的平均成绩(均取整数)如表所示:
| |
60分以下 |
61﹣70分 |
71﹣80分 |
81﹣90分 |
91﹣100分 |
| 甲班(人数) |
3 |
6 |
11 |
18 |
12 |
| 乙班(人数) |
3 |
9 |
13 |
15 |
10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分析估计两个班级的优秀率;
(2)由以上统计列出2×2列联表.
已知函数 .
.
(1)求函数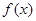 的最小正周期;
的最小正周期;
(2)求函数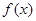 在区间
在区间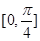 上的函数值的取值范围.
上的函数值的取值范围.
已知椭圆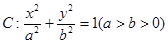 过点
过点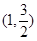 ,且离心率
,且离心率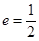 。
。
(Ⅰ)求椭圆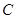 的标准方程;
的标准方程;
(Ⅱ)若直线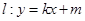 与椭圆
与椭圆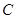 相交于
相交于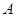 ,
,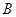 两点(
两点( 不是左右顶点),椭圆的右顶点为D,且满足
不是左右顶点),椭圆的右顶点为D,且满足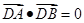 ,试判断直线
,试判断直线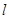 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由。
已知函数 .
.
(I)求函数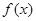 的单调递减区间;
的单调递减区间;
(II)若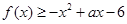 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(III)过点 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程
设数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,数列
,数列 是公差为d的等差数列,
是公差为d的等差数列, .
.
(1)求d的值;
(2)求数列 的通项公式;
的通项公式;
(3)求证: .
.
将边长为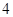 的正方形
的正方形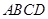 和等腰直角三角形
和等腰直角三角形 按图拼为新的几何图形,
按图拼为新的几何图形,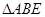 中,
中,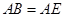 ,连结
,连结 ,若
,若 ,
,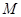 为
为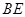 中点
中点
(Ⅰ)求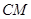 与
与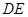 所成角的大小;
所成角的大小;
(Ⅱ)若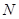 为
为 中点,证明:
中点,证明: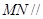 平面
平面 ;
;
(Ⅲ)证明:平面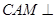 平面
平面