已知在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8.E,F分别是线段A1A,BC上的点.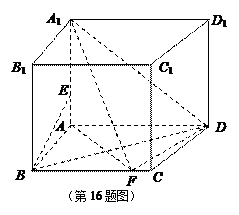
(1)若A1E=5,BF=10,求证:BE∥平面A1FD.
(2)若BD⊥A1F,求三棱锥A1-AB1F的体积.
15.(本小题满分14分)
已知函数f(x)=sin2x+sinxcosx-(xÎR).
(1)若xÎ(0,),求f(x)的最大值;
(2)在△ABC中,若A<B,f(A)=f(B)=,求的值.
(本小题满分12分)
甲、乙两人各射击一次,击中目标的概率分别是和.假设两人射击是否击中目标相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少有1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中 目标3次的概率.
目标3次的概率.
(本小题满分12分)
如图所示,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=,∠ABC=60°.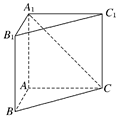
(1)证明:AB⊥A1C;
(2)求二面角A-A1C-B的余弦值.
(本小题满分13分)
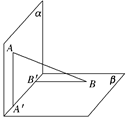
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,若AB=12,求A′B′的长度.