（本小题满分12分）
甲、乙两人各射击一次，击中目标的概率分别是和．假设两人射击是否击中目标相互之间没有影响；每人各次射击是否击中目标，相互之间也没有影响．
(1)求甲射击4次，至少有1次未击中目标的概率；
(2)求两人各射击4次，甲恰好击中目标2次且乙恰好击中
目标3次的概率．
一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球，现从中有放回地随机抽取2个小球，抽取的球的编号分别记为
、
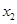，记
.
（Ⅰ）求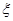
取最大值的概率；
（Ⅱ）求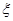的分布列及数学期望.
已知抛物线
，点P（-1，0）是其准线与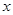
轴的焦点，过P的直线
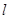与抛物线C交于A、B两点.
（1）当线段AB的中点在直线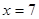
上时，求直线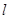的方程；
（2）设F为抛物线C的焦点，当A为线段PB中点时，求△FAB的面积.
四棱锥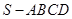
中，底面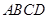
为平行四边形，侧面
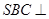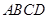底面．已知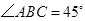
，
，
，
．
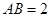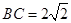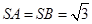（Ⅰ）证明
；
（Ⅱ）求直线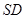
与平面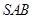
所成角的正弦值.
已知函数
（Ⅰ）若
，求
的极大值；
（Ⅱ）若
在定义域内单调递减，求满足此条件的实数k的取值范围.
已知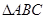
的三个内角
所对的边分别为
,
是锐角,且
．
（Ⅰ）求的度数；
（Ⅱ）若
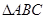，的面积为
，求
的值．