已知二次函数f(x)=ax2+bx+c(a>0).
(Ⅰ)(i)若b=﹣2,且f(x)在(1,+∞)上为单调递增函数,求实数a的取值范围;
(ii)若b=﹣1,c=1,当x∈[0,1]时,|f(x)|的最大值为1,求实数a的取值范围;
(Ⅱ)若f(0)≥1,f(1)≥1,f(x)=0的有两个小于1的不等正根,求a的最小正整数值.
.在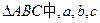 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且
(1)求角B的大小;
(2)设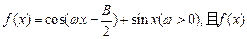 的最小正周期为
的最小正周期为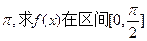 上的最大值和最小值.
上的最大值和最小值.
选修4—5:不等式选讲
2:设 函数
函数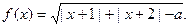
(1)当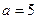 时,求函数
时,求函数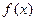 的定义域;
的定义域;
(2)若函数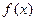 的定义域为R,试求
的定义域为R,试求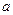 的取值范围。
的取值范围。
(共12分)(考生在下面两题中任选一题解答,若多选则安所做的第一题计分)
选修4—4:坐标系与参数方程
1:已知曲线C的极坐标方程是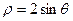 ,设直线
,设直线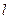 的参数方程是
的参数方程是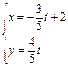 (
( 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线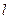 与
与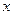 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
(本小题满分12分)
已知F1、F2分别是双曲线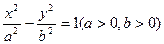 的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H
的左、右焦点,以坐标原点O为圆心,以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A,与y轴正半轴的交点为B,点A在y轴上的射影为H ,且
,且
(I)求双曲线的离心率 ;
;
(II)若AF1交双曲线于点M,且 的值.
的值.
(本小题满分12分)
已知函数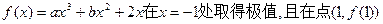 处的切线斜率为2.
处的切线斜率为2.
(I)求 的值;
的值;
(II)若关于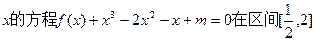 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围.
的取值范围.