综合与探究：
如图，抛物线y=
x2-
x-4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求点A，B，C的坐标．
（2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．
（3）当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
有三张卡片（背面完全相同）分别写有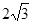
、
、
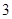，把它们背面朝上洗匀后，小明从中抽取一张，记下这个数后放回洗匀，小白又从中抽出一张．
(1)小明抽取的卡片为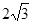的概率是 ；两人抽取的卡片都为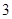的概率是 ．
(2)小刚为他们俩设计了一个游戏规则：若两人抽取的卡片上两数之积是有理数，则小明获胜，否则小白获胜．你认为这个游戏规则对谁有利？请说明理由．
先化简，再求值：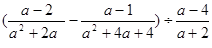
，其中
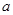满足
.
在直角坐标系x o y中，已知点P是反比例函数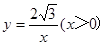
图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．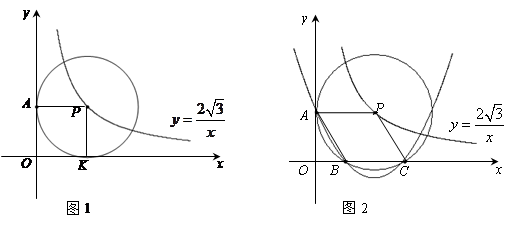
（1）如图1，⊙P运动到与x轴相切时，设切点为K，试判断四边形OKPA的形状，并说明理由．
（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的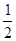
．若存在，请直接写出所有满足条件的M点的坐标，若不存在，试说明理由．
如图，在直角梯形ABCD中，∠A＝90°，∠B＝120°，AD＝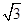
，AB＝6．在底边AB上有一动点E，满足∠DEQ=120°，EQ交射线DC于点F．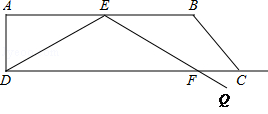
(1)求下底DC的长度；
(2)当点E是AB的中点时，求线段DF的长度；
(3)请计算射线EF经过点C时，AE的长度．
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数
（k≠0）在第一象限内的图象经过点D、E，且tan ∠ BOA=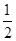
．
（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．