在直角坐标系xOy中,已知点P 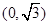 ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为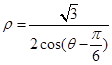 。
。
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与直线C的两个交点为A、B,求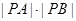 的值。
的值。
(本小题满分12分)定义在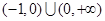 上的函数
上的函数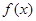 及二次函数
及二次函数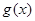 满足:
满足: 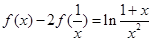 ,
,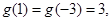 ,且
,且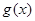 的最小值是
的最小值是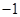 .
.
(Ⅰ)求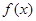 和
和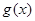 的解析式;
的解析式;
(Ⅱ)若对于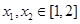 ,均有
,均有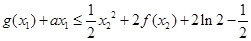 成立,求实数
成立,求实数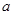 的取值范围;
的取值范围;
(Ⅲ)设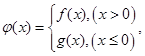 讨论方程
讨论方程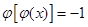 的解的个数情况.
的解的个数情况.
(本小题满分12分)某创业投资公司拟投资开发某种新能源产品,估计能获得投资收益的范围是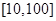 (单位:万元).现准备制定一个对科研课题组的奖励方案:奖金
(单位:万元).现准备制定一个对科研课题组的奖励方案:奖金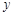 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过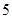 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的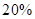 .
.
(Ⅰ)若建立函数模型 制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
(Ⅱ)现有两个奖励函数模型: ;
; .试分析这两个函数模型是否符合公司要求.
.试分析这两个函数模型是否符合公司要求.
(本小题满分12分)设函数 .
.
(Ⅰ)若 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若 ,且
,且 在
在 上的最小值为
上的最小值为 ,求
,求 在该区间上的最大值.
在该区间上的最大值.
(本小题满分10分)已知函数
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若二次函数 与函数
与函数 的图象恒有公共点,求实数
的图象恒有公共点,求实数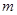 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,
, ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(Ⅰ) ,使得不等式
,使得不等式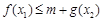 成立,试求实数
成立,试求实数 的取值范围;
的取值范围;
(Ⅱ)若 ,求证:
,求证: .
.