在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 _________ ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.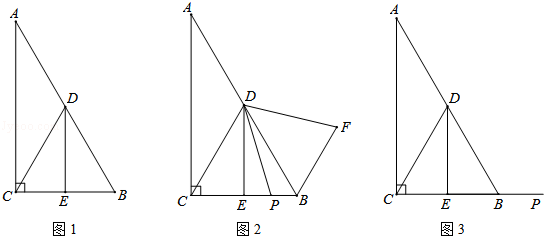
如图,在⊿ABC中,AB=BC,点D在AB的延长线上。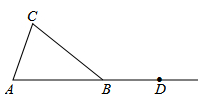
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F.
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由。
先化简,再求值: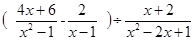 ,其中
,其中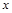 是不等式组
是不等式组 的整数解。
的整数解。
如图,在四边形ABCD中,点E.F.G.H分别为四边形ABCD各边的中点,顺次连接点E.F.G.H,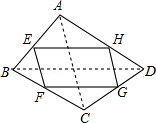
(1)试判断四边形EFGH的形状,并证明你的结论.
(2)如果四边形ABCD是矩形,则四边形EFGH是什么形状?并说明理由.
如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连结DB交CF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由.
如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.