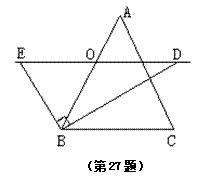
已知梯形ABCD中,AD∥BC,AD=1,BC=2,sinB= ,过点C在∠BCD的内部作射线交射线BA于点E,使得∠DCE=∠B.
,过点C在∠BCD的内部作射线交射线BA于点E,使得∠DCE=∠B.
(1)如图1,当ABCD为等腰梯形时,求AB的长;
(2)当点E与点A重合时(如图2),求AB的长;
(3)当△BCE为直角三角形时,求AB的长.
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图: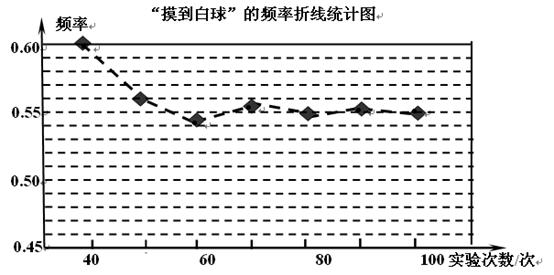
(1)请估计:当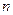 很大时,摸到白球的频率将会接近(精确到0.01);
很大时,摸到白球的频率将会接近(精确到0.01);
(2)假如你摸一次,你摸到黑球的概率P(黑球)=;
(3)试估算盒子里白、黑两种颜色的球各有多 少个?
少个?
(4)在(2)条件下如果要使摸到白球的概率为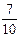 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
如图,在△ABC中,BC>AC,点D在BC上,且DC=AC.
(1)利用直尺与圆规先作∠ACB的平分线,交AD于F点,再作线段AB的垂直
平分线,交AB于点E,最后连结EF(保留作图痕迹,不要求写作法、证明).
(2)若线段AC= 8,BC= 12,求线段EF的长.
先化简,再求值: ,其中x=2sin60°+1.
,其中x=2sin60°+1.
如图,在□ABCD中,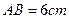 ,
,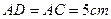 .点
.点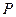 由
由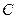 出发沿
出发沿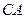 方向匀速运动,速度为
方向匀速运动,速度为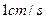 ;同时,线段
;同时,线段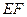 由
由 出发沿
出发沿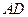 方向匀速运动,速度为
方向匀速运动,速度为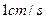 ,交
,交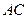 于
于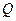 ,连接
,连接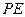 、
、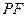 .若设运动时间为
.若设运动时间为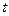 (s)(
(s)(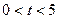 ).解答下列问题:
).解答下列问题:
(1)当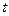 为何值时,
为何值时,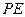 ∥
∥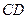 ?并求出此时
?并求出此时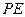 的长;
的长;
(2)试判断△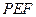 的形状,并请说明理由.
的形状,并请说明理由.
(3)当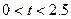 时,
时,
(ⅰ)在上述运动过程中,五边形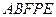 的面积▲(填序号)
的面积▲(填序号)
①变大②变小③先变大,后变小
 ④不变
④不变
(ⅱ)设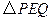 的面积为
的面积为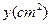 ,求出
,求出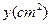 与
与 之间的函数关系式及
之间的函数关系式及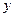 的取值范围.
的取值范围.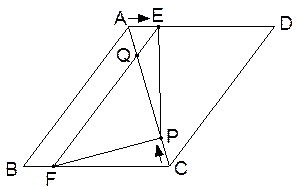
如图,△ABC中,点O在边AB上,过点O作BC的平行线交∠ABC
的平分线于点D,过点B作BE⊥BD,交直线OD于点E。
(1)求证:OE=OD ;
(2)当点O在什么位置时,四边形BDAE是矩形 ?说明理由;
?说明理由;
(3)在满足(2)的条件下,还需△ABC满足什么条件时,四边形BDAE是正方形?写出你确定的条件,并画出图形,不必证明。