如图 在平面直角坐标系
在平面直角坐标系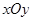 中
中 点
点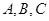 均在单位圆上
均在单位圆上 已知点
已知点 在第一象限的横坐标是
在第一象限的横坐标是 点
点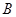 在第二象限
在第二象限 点
点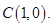
(1)设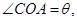 求
求 的值;
的值;
(2)若 为正三角形
为正三角形 求点
求点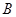 的坐标
的坐标
(本题12分)求过直线 和
和 的交点,且垂直于直线
的交点,且垂直于直线 的直线方程。
的直线方程。
(本题12分)已知函数
(1)判断 的奇偶性;
的奇偶性;
(2)判断并用定义证明 在
在 上的单调性。
上的单调性。
(本小题满分 分)
分)
已知函数 .(
.( 为常数,
为常数, )
)
(Ⅰ)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(Ⅱ)求证:当 时,
时, 在
在 上是增函数;
上是增函数;
(Ⅲ)若对任意的 ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分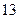 分)
分)
已知数列 满足
满足
(Ⅰ)李四同学欲求 的通项公式,他想,如能找到一个函数
的通项公式,他想,如能找到一个函数



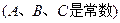 ,把递推关系变成
,把递推关系变成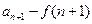
 后,就容易求出
后,就容易求出 的通项了.请问:他设想的
的通项了.请问:他设想的 存在吗?
存在吗? 的通项公式是什么?
的通项公式是什么?
(Ⅱ)记 ,若不等式
,若不等式 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围
的取值范围
(本小题满分 分)
分)
已知双曲线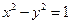 的左、右顶点分别为
的左、右顶点分别为 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
(Ⅰ)求 的取值范围,并求
的取值范围,并求 的最小值;
的最小值;
(Ⅱ)记直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明