如图，点E为平行四边形ABCD中DC延长线上的一点，且CED-优题课

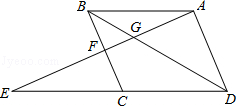
（1）【探究发现】

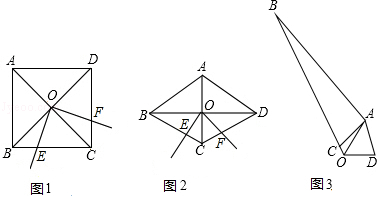
如图1，∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处，∠ EOF＝90°，将∠ EOF绕点 O旋转，旋转过程中，∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F（点 F与点 C， D不重合）．则 CE， CF， BC之间满足的数量关系是　　．

（2）【类比应用】

如图2，若将（1）中的"正方形 ABCD"改为"∠ BCD＝120°的菱形 ABCD"，其他条件不变，当∠ EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由．

（3）【拓展延伸】

如图3，∠ BOD＝120°， OD＝ $\frac{3}{4}$ ， OB＝4， OA平分∠ BOD， AB＝ $\sqrt{13}$ ，且 OB＞2 OA，点 C是 OB上一点，∠ CAD＝60°，求 OC的长．

某工厂制作 A， B两种手工艺品， B每件获利比 A多105元，获利30元的 A与获利240元的 B数量相等．

（1）制作一件 A和一件 B分别获利多少元？

（2）工厂安排65人制作 A， B两种手工艺品，每人每天制作2件 A或1件 B．现在在不增加工人的情况下，增加制作 C．已知每人每天可制作1件 C（每人每天只能制作一种手工艺品），要求每天制作 A， C两种手工艺品的数量相等．设每天安排 x人制作 B， y人制作 A，写出 y与 x之间的函数关系式．

（3）在（1）（2）的条件下，每天制作 B不少于5件．当每天制作5件时，每件获利不变．若每增加1件，则当天平均每件获利减少2元．已知 C每件获利30元，求每天制作三种手工艺品可获得的总利润 W（元）的最大值及相应 x的值．

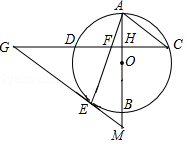
如图， AB是⊙ O的直径，弦 CD⊥ AB，垂足为 H，连接 AC．过 $\overset{⏜}{BD}$ 上一点 E作 EG∥ AC交 CD的延长线于点 G，连接 AE交 CD于点 F，且 EG＝ FG．

（1）求证： EG是⊙ O的切线；

（2）延长 AB交 GE的延长线于点 M，若 AH＝2， CH＝2 $\sqrt{2}$ ，求 OM的长．

某校组织学生到恩格贝 A和康镇 B进行研学活动，澄澄老师在网上查得， A和 B分

别位于学校 D的正北和正东方向， B位于 A南偏东37°方向，校车从 D出发，沿正北方向前往 A地，行驶到15千米的 E处时，导航显示，在 E处北偏东45°方向有一服务区 C，且 C位于 A， B两地中点处．

（1）求 E， A两地之间的距离；

（2）校车从 A地匀速行驶1小时40分钟到达 B地，若这段路程限速100千米/时，计算校车是否超速？

（参考数据：sin37°＝ $\frac{3}{5}$ ，cos37°＝ $\frac{4}{5}$ ，tan37°＝ $\frac{3}{4}$ ）

教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃停止加热，水温开始下降，此时水温 y（℃）与开机后用时 x（ min）成反比例关系，直至水温降至30℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时接通电源，水温 y（℃）与时间 x（ min）的关系如图所示：

（1）分别写出水温上升和下降阶段 y与 x之间的函数关系式；

（2）怡萱同学想喝高于50℃的水，请问她最多需要等待多长时间？