如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=2 .
.
(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC;
(3)求三棱锥B﹣DOM的体积.
设集合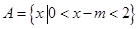 ,
,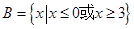 .分别求出满足下列条件的实数
.分别求出满足下列条件的实数 的取值范围.
的取值范围.
(Ⅰ)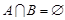 ;
;
(Ⅱ) .
.
已知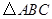 的顶点
的顶点 在椭圆
在椭圆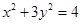 上,
上, 在直线
在直线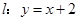 上,且
上,且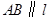 .
.
(1)当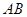 边通过坐标原点
边通过坐标原点 时,求
时,求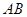 的长及
的长及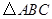 的面积;
的面积;
(2)当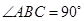 ,且斜边
,且斜边 的长最大时,求
的长最大时,求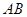 所在直线的方程.
所在直线的方程.
如图,直线y=kx+b与椭圆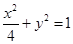 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.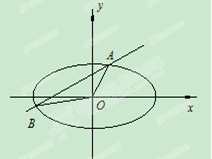
(1)求在k=0,0<b<1的条件下,S的最大值;
(2)当|AB|=2,S=1时,求直线AB的方程.
在平面直角坐标系xOy中,直线l与抛物线y2=4x相交于不同的A、B两点.
(1)如果直线l过抛物线的焦点,求 ·
· 的值;
的值;
(2)如果 ·
· =-4,证明直线l必过一定点,并求出该定点.
=-4,证明直线l必过一定点,并求出该定点.
已知椭圆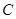 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆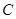 的方程;
的方程;
(2)若 为椭圆
为椭圆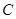 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,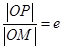 (
(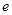 为椭圆的离心率),求点
为椭圆的离心率),求点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.