数列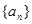 的前
的前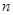 项和为
项和为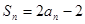 ,
,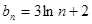 ,函数
,函数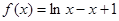 .
.
(1)求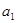 的值和数列
的值和数列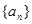 的通项公式;
的通项公式;
(2)证明:当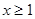 时,
时,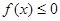 ;
;
(3)求证: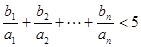 .
.
(本小题满分12分)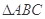 为等腰直角三角形,
为等腰直角三角形,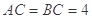 ,
,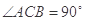 ,
,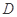 、
、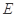 分别是边
分别是边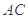 和
和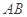 的中点,现将
的中点,现将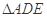 沿
沿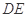 折起,使面
折起,使面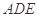
 面
面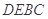 ,
,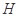 、
、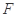 分别是边
分别是边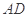
和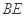 的中点,平面
的中点,平面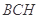 与
与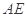 、
、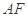 分别交于
分别交于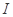 、
、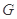 两点.
两点.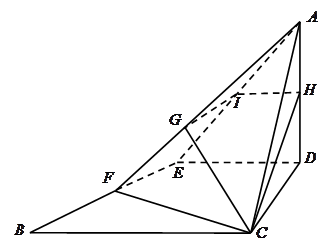
(Ⅰ)求证: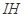
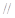
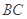 ;
;
(Ⅱ)求二面角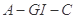 的余弦值;
的余弦值;
(Ⅲ)求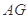 的长.
的长.
(本小题满分12分)已知数列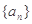 满足
满足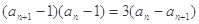 ,
,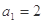 ,令
,令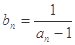 .
.
(Ⅰ)证明:数列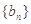 是等差数列;
是等差数列;
(Ⅱ)求数列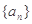 的通项公式.
的通项公式.
(本小题满分12分)设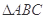 是锐角三角形,三个内角
是锐角三角形,三个内角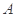 ,
,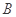 ,
,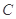 所对的边分别记为
所对的边分别记为 ,
,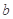 ,
,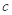 ,并且
,并且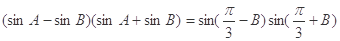 .
.
(Ⅰ)求角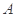 的值;
的值;
(Ⅱ)若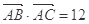 ,
,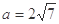 ,求
,求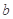 ,
,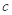 (其中
(其中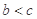 ).
).
(本小题满分10分)选修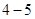 :不等式选讲
:不等式选讲
已知函数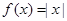 ,
,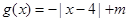
(Ⅰ)解关于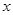 的不等式
的不等式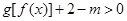 ;
;
(Ⅱ)若函数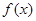 的图像恒在函数
的图像恒在函数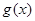 图像的上方,求实数
图像的上方,求实数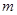 的取值范围.
的取值范围.
(本小题满分10分)选修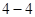 ;坐标系与参数方程
;坐标系与参数方程
在直角坐标系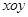 中,以坐标原点为极点,
中,以坐标原点为极点,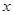 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为: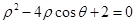 .
.
(Ⅰ)将极坐标方程化为普通方程;
(Ⅱ)若点P(x,y)在该圆上,求x+y的最大值和最小值.