(本小题满分12分)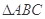 为等腰直角三角形,
为等腰直角三角形,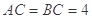 ,
,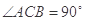 ,
,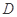 、
、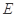 分别是边
分别是边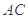 和
和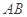 的中点,现将
的中点,现将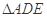 沿
沿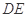 折起,使面
折起,使面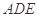
 面
面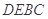 ,
,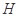 、
、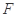 分别是边
分别是边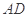
和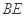 的中点,平面
的中点,平面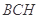 与
与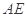 、
、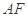 分别交于
分别交于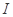 、
、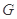 两点.
两点.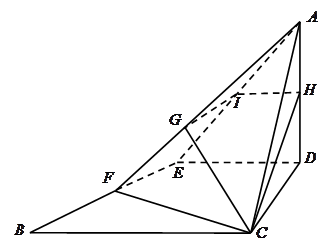
(Ⅰ)求证: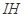
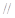
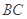 ;
;
(Ⅱ)求二面角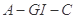 的余弦值;
的余弦值;
(Ⅲ)求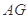 的长.
的长.
(本小题满分8分)已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、
黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)列出一次任取2个球的所有基本事件;
(3)从中取2个球,求至少有一个红球的概率.
(本小题满分8分)已知角 的终边在
的终边在 上,求
上,求
(1) 的值;
的值;
(2)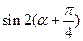 的值.
的值.
已知二次函数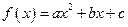 满足条件:①
满足条件:① 是
是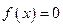 的两个零点;②
的两个零点;②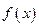 的最小值为
的最小值为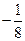
(1)求函数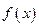 的解析式;
的解析式;
(2)设数列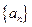 的前
的前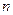 项积为
项积为 ,且
,且 ,
,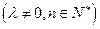 ,求数列
,求数列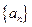 的前
的前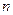 项和
项和
(3)在(2)的条件下,当 时,若
时,若 是
是 与
与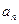 的等差中项,试问数列
的等差中项,试问数列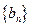 中
中
第几项的值最小?并求出这个最小值。
已知函数 。
。
(I)若从集合{0,1,2,3}中任取一个元素作为 ,从集合{0,1,2}中任取一个元素作为b,求方程
,从集合{0,1,2}中任取一个元素作为b,求方程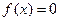 有两个不等实数根的概率;
有两个不等实数根的概率;
(II)若从区间[0,2]中任取一个数作为 ,从区间
,从区间 中任取一个数作为
中任取一个数作为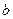 ,求方程
,求方程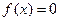 没有实数根的概率。
没有实数根的概率。
已知抛物线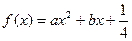 与直线
与直线 相切于点A(1,1)。
相切于点A(1,1)。
(1)求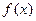 的解析式;
的解析式;
(2)若对任意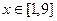 ,不等式
,不等式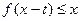 恒成立,求实数
恒成立,求实数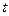 的取值范围。
的取值范围。