(本小题满分10分)选修 ;坐标系与参数方程
;坐标系与参数方程
在直角坐标系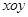 中,以坐标原点为极点,
中,以坐标原点为极点,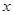 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为: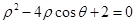 .
.
(Ⅰ)将极坐标方程化为普通方程;
(Ⅱ)若点P(x,y)在该圆上,求x+y的最大值和最小值.
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| 专业A |
专业B |
总计 |
|
| 女生 |
12 |
4 |
16 |
| 男生 |
38 |
46 |
84 |
| 总计 |
50 |
50 |
100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=
| P(K2≥k0) |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k0 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=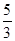 ,D(η)=
,D(η)= ,求a∶b∶c.
,求a∶b∶c.
假设某班级教室共有4扇窗户,在每天上午第三节课上课预备铃声响起时,每扇窗户或被敞开或被关闭,且概率均为0.5.记此时教室里敞开的窗户个数为X.
(1)求X的分布列;
(2)若此时教室里有两扇或两扇以上的窗户被关闭,班长就会将关闭的窗户全部敞开,否则维持原状不变.记每天上午第三节课上课时该教室里敞开的窗户个数为Y,求Y的数学期望.
一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4;白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片(假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率;
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.