已知函数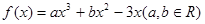 ,在点
,在点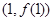 处的切线方程为
处的切线方程为 .
.
(I)求函数 的解析式;
的解析式;
(II)若对于区间 上任意两个自变量的值
上任意两个自变量的值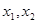 ,都有
,都有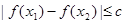 ,求实数
,求实数 的最小值;
的最小值;
(III)若过点 ,可作曲线
,可作曲线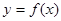 的三条切线,求实数
的三条切线,求实数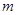 的取值范围.
的取值范围.
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为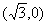 .
.
(1) 求双曲线C的方程;
(2) 若直线l: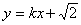 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
建立极坐标系证明:已知半圆直径|AB|=2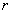 (
(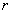 >0),半圆外一条直线
>0),半圆外一条直线 与AB所在直线垂直相交于点T,并且∣AT|=2
与AB所在直线垂直相交于点T,并且∣AT|=2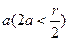 .若半圆上相异两点M.N到
.若半圆上相异两点M.N到 的距离|MP|,|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1,则|MA|+|NA|=|AB|.
的距离|MP|,|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1,则|MA|+|NA|=|AB|.
在平面直角坐标系中已知点A(3,0),P是圆珠笔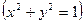 上一个运点,且
上一个运点,且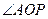 的平分线交PA于Q点,求Q 点的轨迹的极坐标方程.
的平分线交PA于Q点,求Q 点的轨迹的极坐标方程.
若不计空气阻力,炮弹运行轨道是抛物线.现测得我炮位A与炮击目标B在同一水平线上,水平距离为6000米,炮弹运行的最大高度为1200米.试求炮弹的发射角α的正切值和发射初速度v0(重力加速度g=9.8米/秒2).
设椭圆4x2+y2=1的平行弦的斜率为2,求这组平行弦中点的轨迹.