建立极坐标系证明:已知半圆直径|AB|=2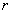 (
(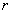 >0),半圆外一条直线
>0),半圆外一条直线 与AB所在直线垂直相交于点T,并且∣AT|=2
与AB所在直线垂直相交于点T,并且∣AT|=2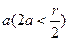 .若半圆上相异两点M.N到
.若半圆上相异两点M.N到 的距离|MP|,|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1,则|MA|+|NA|=|AB|.
的距离|MP|,|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1,则|MA|+|NA|=|AB|.
学校游园活动有这样一个游戏节目,甲箱子里装有3个白球、2个黑球;乙箱子里装有
1个白球、2个黑球。这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在一次游戏中:
①摸出3个白球的概率;
②获奖的概率;
(Ⅱ)求在两次游戏中获奖次数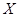 的分布列及数学期望
的分布列及数学期望 .
.
如图,直三棱柱 中,
中, ,
, ,
, 是棱
是棱 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的余弦值。
的余弦值。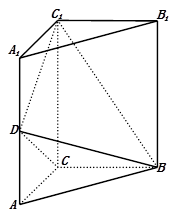
已知函数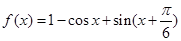 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)记 得内角
得内角 的对应边为
的对应边为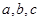 ,若
,若 求
求 的值.
的值.
已知二次函数 中
中 均为实数,且满足
均为实数,且满足 ,对于任意实数
,对于任意实数 都有
都有 ,并且当
,并且当 时有
时有 成立。
成立。
(1)求 的值;
的值;
(2)证明: ;
;
(3)当 ∈[-2,2]且
∈[-2,2]且 取最小值时,函数
取最小值时,函数 (
( 为实数)是单调函数,求证:
为实数)是单调函数,求证: 。
。
已知定义域为R的函数 是奇函数。
是奇函数。
(1)求 的值;
的值;
(2)用定义证明 在
在
 上为减函数;
上为减函数;
(3)若对于任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。