在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
| 作物产量(kg) |
300 |
500 |
| 概率 |
0.5 |
0.6 |
| 作物市场价格(元/kg) |
6 |
10 |
| 概率 |
0.4 |
0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
.(本题满分12分)
先后抛掷一枚质地均匀的骰子(骰子的六个面上分别标以数字 ),骰子向上的数字依次记为
),骰子向上的数字依次记为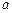 、
、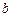 .
.
(Ⅰ)求 能被3整除的概率;
能被3整除的概率;
(Ⅱ)求使关于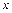 的方程
的方程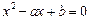 有实数解的概率;
有实数解的概率;
(Ⅲ)求使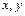 方程组
方程组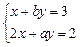 有正数解的概率.
有正数解的概率.
(本题满分10分)
已知某种钻石的价值υ(万元)与其重量ω (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为35万元.
(Ⅰ)写出υ关于ω的函数关系式;
(Ⅱ)若把一颗钻石切割成重量比为1∶3的两颗钻石,求价值损失的百分率;
(Ⅲ)请猜想把一颗钻石切割成两颗钻石时,按重量比为多少时价值损失的百分率最大?(直接写出结果,不用证明)(注:价值损失的百分率=
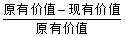 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)
为了解某校高一年级女生的身高情况,选取一个容量为80的样本(80名女生 的身高,单位:cm),分组情况如下:
的身高,单位:cm),分组情况如下:
| 分组 |
151.5~158.5 |
158.5~1 65.5 65.5 |
165.5~172.5 |
172.5~179.5 |
| 频数 |
12 |
24 |
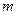 |
|
| 频率 |
 |
0.15 |
(Ⅰ)求出表中
 ,
,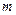 的值,并画出频率分布直方图;
的值,并画出频率分布直方图;
(Ⅱ)试估计身高高于162.0cm的女生的比例.
设
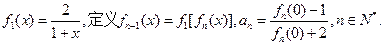
(1)写出 的递推关系式,并求出
的递推关系式,并求出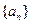 的通项公式;
的通项公式;
(2)若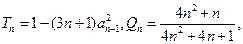 试比较
试比较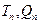 大小
大小 并证明
并证明
设 ,函数
,函数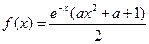 ,其中e是自然对数的底数。
,其中e是自然对数的底数。
(1)求a=-1时,求 在[-1,2]上的最小值;
在[-1,2]上的最小值;
(2)求函数 在R上的单调区间;
在R上的单调区间;
(3)若a为常数,且 是否存在实数t,使得对于任意
是否存在实数t,使得对于任意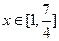 ,
, 恒成立,存在,求出t的范围,不存在,说明理由。
恒成立,存在,求出t的范围,不存在,说明理由。