（本小题满分12分）
某工厂生产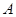
、
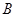两种产品，计划每种产品的生产量不少于15千克，已知生产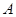产品1千克要用煤9吨，电力4千瓦，3个工作日；生产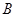产品1千克要用煤4吨，电力5千瓦，10个工作日。又知生产出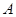产品1千克可获利7万元，生产出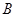产品1千克可获利12万元，现在工厂只有煤360吨，电力200千瓦，300个工作日，
（1）列出满足题意的不等式组，并画图；
（2）在这种情况下,生产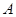、B产品各多少千克能获得最大经济效益.
已知椭圆G：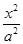
＋
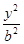＝1（a＞b＞0）的离心率为
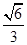，右焦点为（2
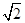，0）．斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P（－3,2）．
（1）求椭圆G的方程；
（2）（有一点难度哦）求△PAB的面积．
已知a、b、c∈R，求证：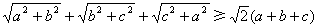
已知x,y∈（－
，）且xy＝－1，求
的最小值。
在平面直角坐标系xOy中，已知圆x2＋y2－12x＋32＝0的圆心为Q，过点P（0,2），且斜率为k的直线与圆Q相交于不同的两点A，B.
（1）求k的取值范围；
（2）是否存在常数k，使得向量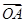
＋
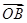与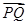
共线？如果存在，求k值；如果不存在，请说明理由．
（高考真题）已知函数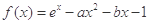
，其中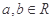
，
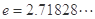为自然对数的底数。
（1）设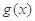
是函数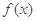
的导函数，求函数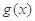在区间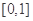
上的最小值；
（2）（能力提升）若
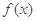，函数在区间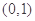
内有零点，求
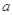的取值范围