设函数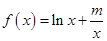 ,
,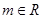 .
.
(1)当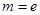 (
(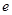 为自然对数的底数)时,求
为自然对数的底数)时,求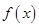 的极小值;
的极小值;
(2)讨论函数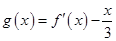 零点的个数.
零点的个数.
已知函数 ,
,  ,
,
(Ⅰ)设函数 ,
,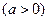 ,若函数
,若函数 没有零点,求
没有零点,求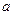 的取值范围;(Ⅱ)若总有
的取值范围;(Ⅱ)若总有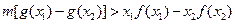 成立,求实数
成立,求实数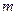 的取值范围.
的取值范围.
已知数列 的前n项和为
的前n项和为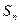 ,且满足
,且满足
(Ⅰ)求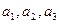 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若 ,数列
,数列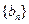 的前n项和为
的前n项和为 求满足不等式
求满足不等式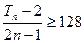 的最小n值.
的最小n值.
如图,已知 平面
平面 是正三角形,
是正三角形,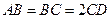 。
。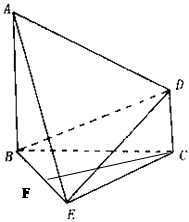 (Ⅰ)若
(Ⅰ)若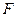 是
是 的中点,求证
的中点,求证 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成的角的正切值。
所成的角的正切值。
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果;
(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 .已知
.已知 .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求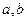 ;
;
(Ⅱ)若 ,求
,求 的面积.
的面积.