如图,已知⊙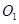 与⊙
与⊙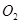 相交于
相交于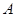 、
、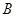 两点,过点A作⊙
两点,过点A作⊙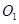 的切线交⊙O2于点
的切线交⊙O2于点 ,过点
,过点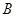 作两圆的割线,分别交⊙
作两圆的割线,分别交⊙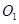 、⊙
、⊙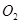 于点
于点 、
、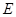 ,
,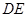 与
与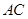 相交于点
相交于点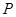 .[来源
.[来源
(1)求证: ;
;
(2)若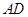 是⊙
是⊙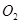 的切线,且
的切线,且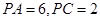 ,
,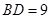 ,求
,求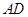 的长.
的长.
如图,某观测站 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东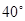 ,在
,在 处测得距
处测得距 为31公里的公路上
为31公里的公路上 处,有一人正沿公路向
处,有一人正沿公路向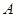 城走去,走了20公里后,到达
城走去,走了20公里后,到达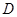 处,此时
处,此时 、
、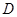 间距离为
间距离为 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达 城.
城.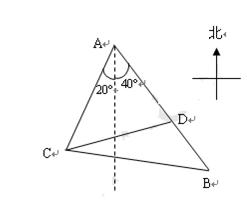
制订投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损,某投资人打算投资甲、乙两个项目,根据预测,甲、乙两个项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损率分别为30﹪和10﹪,若投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
已知 、
、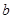 、
、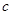 分别是
分别是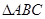 的三个内角
的三个内角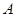 、
、 、
、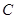 所对的边;
所对的边;
(1)若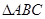 面积
面积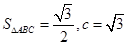 ,且
,且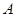 、
、 、
、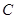 成等差数列,求
成等差数列,求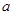 、
、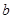 的值;
的值;
(2)若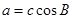 ,且
,且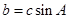 ,试判断
,试判断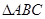 的形状。
的形状。
已知等差数列 中,
中,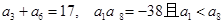 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)调整数列 的前三项
的前三项 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 的前
的前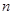 项和.
项和.
(本小题满分12分)
已知
(1)求 的值;
的值;
(2)当 (其中
(其中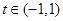 ,且
,且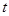 为常数)时,
为常数)时,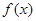 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如
果不存在,请说明理由;
(3)当 时,求满足不等式
时,求满足不等式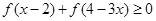 的
的 的范围.
的范围.