已知抛物线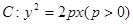 ,
,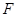 为抛物线
为抛物线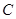 的焦点,
的焦点, 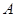 为抛物线
为抛物线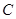 上的动点,过
上的动点,过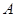 作抛物线准线
作抛物线准线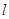 的垂线,垂足为
的垂线,垂足为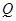 .
.
(1)若点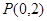 与点
与点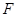 的连线恰好过点
的连线恰好过点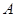 ,且
,且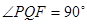 ,求抛物线方程;
,求抛物线方程;
(2)设点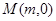 在
在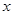 轴上,若要使
轴上,若要使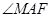 总为锐角,求
总为锐角,求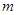 的取值范围.
的取值范围.
(本大题9分)
求满足下列条件的直线方程:
(1)经过点P(2,-1)且与直线2x+3y+12=0平行;
(2)经过点Q(-1,3)且与直线x+2y-1=0垂直;
(3)经过点M(1,2)且与点A(2,3)、B(4,-5)距离相等;
(4)经过点N(-1, 3)且在
3)且在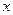 轴的截距与它在y轴上的截距的和为零.
轴的截距与它在y轴上的截距的和为零.
(本大题8分)已知正方体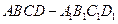 ,求:
,求:
(1)异面直线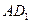 与
与 所成的角;
所成的角;
(2)证明:直线 //平面
//平面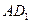 C
C
(3)二面角D— A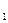 B—C
B—C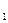 的大小;
的大小;
(本大题8分)
在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足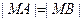 ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
(本大题8分)
命题 方程
方程 有两个不等的正实数根,命题
有两个不等的正实数根,命题 方程
方程 无实数根。若“
无实数根。若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
已知圆 与直线
与直线 相交于P、Q两点,O为原点,且
相交于P、Q两点,O为原点,且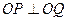 ,求实数
,求实数 的值。
的值。