若函数 ,当
,当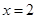 时,函数
时,函数 有极值-
有极值- .求函数
.求函数 的解析式.
的解析式.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.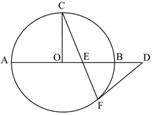
(1)求证:DE2=DB•DA;
(2)若DB=2,DF=4,试求CE的长.
已知函数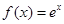 ,
,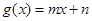 .
.
(1)设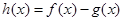 .
.
①若函数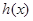 在
在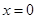 处的切线过点
处的切线过点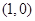 ,求
,求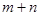 的值;
的值;
②当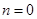 时,若函数
时,若函数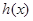 在
在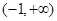 上没有零点,求
上没有零点,求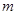 的取值范围;
的取值范围;
(2)设函数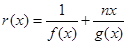 ,且
,且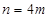 (
(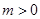 ),求证:当
),求证:当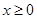 时,
时,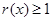 .
.
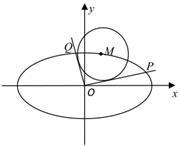
如图,已知 是椭圆
是椭圆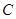 :
: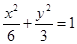 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: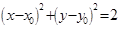 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 、
、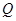 .
.
(1)若直线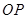 ,
,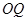 的斜率存在,并记为
的斜率存在,并记为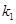 ,
,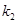 ,求证:
,求证: 为定值;
为定值;
(2)试问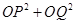 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
如图,在四棱锥 中,底面梯形
中,底面梯形 中,
中, ,平面
,平面 平面
平面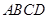 ,
,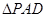 是等边三角形,已知
是等边三角形,已知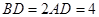 ,
, ,
, ,且
,且 .
.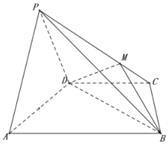
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)试确定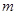 的值,使三棱锥
的值,使三棱锥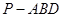 体积为三棱锥
体积为三棱锥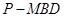 体积的3倍.
体积的3倍.
已知 的角
的角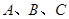 的对边分别为
的对边分别为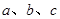 ,其面积
,其面积 ,
,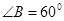 ,且
,且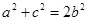 ;等差数列
;等差数列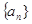 中,且
中,且 ,公差
,公差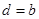 .数列
.数列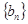 的前
的前 项和为
项和为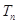 ,且
,且 ,
,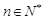 .
.
(1)求数列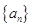 、
、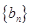 的通项公式;
的通项公式;
(2)设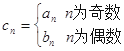 , 求数列
, 求数列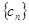 的前
的前 项和
项和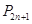 .
.