每年5月17日为国际电信日,某市电信公司在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.电信日当天参与活动的人数统计结果如图所示,现将频率视为概率.
(1) 求某人获得优惠金额不低于300元的概率;
(2) 若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出两人,求这两人获得相等优惠金额的概率.
已知全集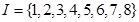 ,其中
,其中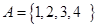 ,
,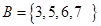
(1)求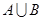
 (2) 求
(2) 求 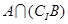
已知定义在 的函数
的函数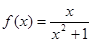
(1)试判断 的奇偶性。
的奇偶性。
(2)若函数在 上为增函数,解关于
上为增函数,解关于 的不等式
的不等式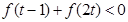 。
。
某车间生产一种仪器的固定成本是10000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数: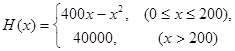 ,其中
,其中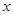 是仪器的月产量(总收入=总成本+利润).
是仪器的月产量(总收入=总成本+利润).
(Ⅰ)将利润(用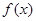 表示)表示为月产量
表示)表示为月产量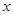 的函数;
的函数;
(Ⅱ)当月产量为何值时,车间所获利润最大?最大利润是多少元?
已知函数 在
在 上有最大值1和最小值0,设
上有最大值1和最小值0,设 (
(
为自然对数的底数).
(1)求 的值;
的值;
(2)若不等式 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
已知数列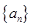 中,
中,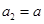 (
( 为非零常数),其前n项和
为非零常数),其前n项和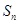 满足
满足 .
.
(1)求数列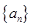 的通项公式;
的通项公式;
(2)若 ,且
,且 ,求
,求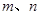 的值;
的值;
(3)是否存在实数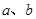 ,使得对任意正整数
,使得对任意正整数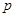 ,数列
,数列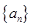 中满足
中满足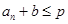 的最大项恰为第
的最大项恰为第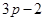 项?
项?
若存在,分别求出 与
与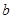 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.