已知数列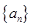 中,
中,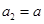 (
( 为非零常数),其前n项和
为非零常数),其前n项和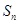 满足
满足 .
.
(1)求数列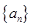 的通项公式;
的通项公式;
(2)若 ,且
,且 ,求
,求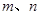 的值;
的值;
(3)是否存在实数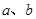 ,使得对任意正整数
,使得对任意正整数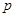 ,数列
,数列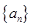 中满足
中满足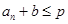 的最大项恰为第
的最大项恰为第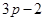 项?
项?
若存在,分别求出 与
与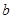 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
设函数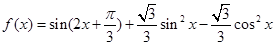
(1) 求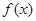 的最小正周期及其图像的对称轴方程;
的最小正周期及其图像的对称轴方程;
(2) 将函数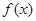 的图像向右平移
的图像向右平移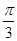 个单位长度,得到函数
个单位长度,得到函数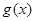 的图像,求
的图像,求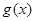 在区间
在区间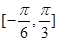 的值域.
的值域.
设数列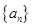 ,
,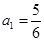 ,若以
,若以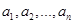 为系数的二次方程:
为系数的二次方程: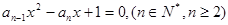 都有根
都有根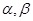 满足
满足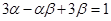 .
.
(1)求证: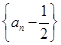 为等比数列
为等比数列
(2)求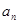 .
.
(3)求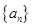 的前
的前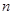 项和
项和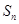 .
.
在△ 中,角
中,角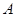 ,
,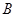 ,
,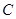 对应的边分别是
对应的边分别是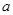 ,
, ,
,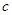 .已知
.已知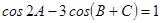 .
.
(1)求角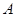 的大小;
的大小;
(2)若△ 的面积
的面积 ,
,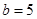 ,求
,求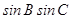 的值.
的值.
设函数
(1)解不等式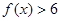 ;
;
(2)若关于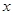 的不等式
的不等式 的解集不是空集,求
的解集不是空集,求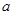 得取值范围.
得取值范围.
以直角坐标系的原点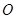 为极点,
为极点,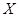 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点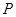 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点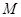 的极坐标为
的极坐标为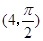 .若直线
.若直线 过点
过点 ,且倾斜角为
,且倾斜角为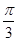 ,圆
,圆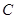 以
以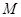 为圆心、4为半径.
为圆心、4为半径.
(1)求直线 的参数方程和圆
的参数方程和圆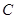 的极坐标方程;
的极坐标方程;
(2)试判定直线 和圆
和圆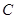 的位置关系.
的位置关系.