山东省第23届运动会在济宁隆重开幕，根据大会组委会安排，某校接受了开幕式大型团体操表演任务．为此，学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商．经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元．经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费．另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人．
（1）分别写出学校购买A、B两公司服装所付的总费用y1（元）和y2（元）与参演男生人数x之间的函数关系式；
（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由．
在一只不透明的布袋中装有红球、黄球各若干个，这些球除颜色外都相同，均匀摇匀.
（1）若布袋中有3个红球，1个黄球．从布袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）；
（2）若布袋中有3个红球，x个黄球．
请写出一个x的值，使得事件“从布袋中一次摸出4个球，都是黄球”是不可能的事件；
（3）若布袋中有3个红球，4个黄球．
我们知道：“从袋中一次摸出4个球，至少有一个黄球”为必然事件．
请你仿照这个表述，设计一个必然事件：．
为了了解“通话时长”（“通话时长”指每次通话时间）的分布情况，小强收集了他家1000个“通话时长”数据，这些数据均不超过18（分钟）．他从中随机抽取了若干个数据作为样本，统计结果如下表，并绘制了不完整的频数分布直方图．
| “通话时长” （x分钟） |
0＜x≤3 |
3＜x≤6 |
6＜x≤9 |
9＜x≤12 |
12＜x≤15 |
15＜x≤18 |
| 次数 |
36 |
a |
8 |
12 |
8 |
12 |
根据表、图提供的信息，解答下面的问题：
（1）a=，样本容量是；
（2）求样本中“通话时长”不超过9分钟的频率：；
（3）请估计小强家这1000次通话中“通话时长”超过15分钟的次数．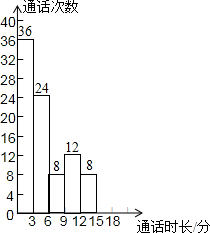
如图，在四边形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，点E在AO上，且OE=OC.
（1）求证：∠1=∠2；
（2）连结BE、DE，判断四边形BCDE的形状，并说明理由.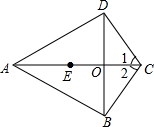
化简：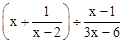
．
读取表格中的信息，解决问题.
| n=1 |
 |
 |
 |
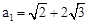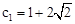| n=2 |
a2=b1+2c1 |
b2=c1+2a1 |
c2=a1+2b1 |
| n=3 |
a3=b2+2c2 |
b3=c2+2a2 |
c=a2+2b2 |
| … |
… |
… |
… |
满足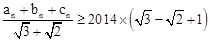
的n可以取得的最小整数是．