如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.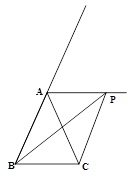
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.
如图是由边长都是1的小正方形组成的网格.请以图中线段BC为边,作△PBC,使P在格点上,并满足:
(1)图甲中的△PBC是直角三角形,且面积是△ABC面积2倍;
(2)图乙中的△PBC是等腰非直角三角形.
分解因式:
(1)(2a+1)2-(2a+1)(-1+2a)
(2)4(x+y)2-(x-y)2
计算:
(1)已知:(x+2)2=25,求x;
(2)计算:
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.