已知函数f(x)=ax-1-ln x(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在x=1处取得极值,不等式f(x)≥bx-2对∀x∈(0,+∞)恒成立,求实数b的取值范围;
(3)当x>y>e-1时,证明不等式exln(1+y)>eyln(1+x).
(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量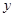 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为
(千米/小时)的函数解析式可以表示为
已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本小题满分12分)
(Ⅰ) 设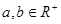 ,求证:
,求证: ;
;
(Ⅱ) 已知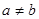 ,求证:
,求证: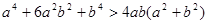
(本小题满分12分)
在各项均为正数的等比数列 中, 已知
中, 已知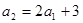 , 且
, 且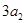 ,
, ,
,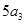 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设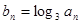 ,求数列
,求数列 的前
的前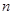 项和
项和 .
.
(本小题满分12分)
如图, ⊿ABC中,D为边AB上的点,∠CAD="60°," CD="21,"
CB="31," DB=20.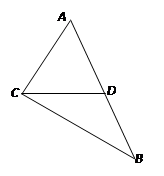
(Ⅰ)记∠CDB= , 求
, 求 ;
;
(Ⅱ)求AD的长.
(本小题共14分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为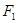 ,
, , 点
, 点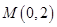 是椭圆的一个顶点,△
是椭圆的一个顶点,△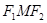 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线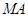 ,
, 交椭圆于
交椭圆于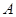 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为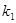 ,
,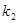 ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).