已知正三棱柱ABC –A1B1C1中,AB = 2,AA1 =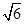 ,点F,E分别是边A1C1和侧棱BB1的中点.
,点F,E分别是边A1C1和侧棱BB1的中点.
(Ⅰ)证明:FB⊥平面AEC;
(Ⅱ)求二面角F-AE-C的余弦值.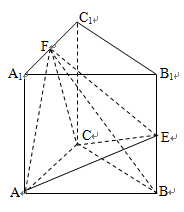
已知函数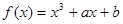 的图象是曲线C,直线
的图象是曲线C,直线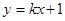 与曲线
与曲线
C相切于点(1,3).
(1)求函数 的解析式;
的解析式;
(2)求函数 的递增区间;
的递增区间;
(3)求函数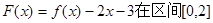 上的最大值和最小值.
上的最大值和最小值.
某饮料公司对一名员工进行测试以便确定其考评级别,公司准备了
两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为
B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工
3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设
此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
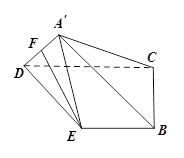
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ADE沿直线DE翻折成△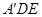 ,使平面
,使平面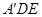 ⊥平面BCDE,F为线段
⊥平面BCDE,F为线段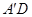 的中点.
的中点.
(Ⅰ)求证:EF∥平面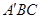 ;
;
(Ⅱ)求直线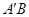 与平面
与平面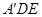 所成角的正切值.
所成角的正切值. 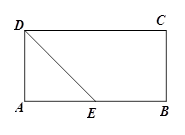
在如图所示的几何体中,四边形ABCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.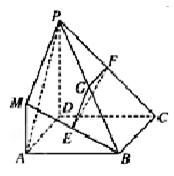
(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
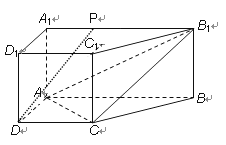
如图所示,直棱柱 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
(1)求证: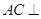 平面
平面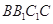 ;
;
(2)在A1B1上是否存一点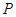 ,使得
,使得 与平面
与平面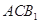 平行?证明你的结论.
平行?证明你的结论.