在等差数列 中,
中,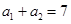 ,
,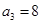 .令
.令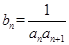 ,数列
,数列 的前
的前 项和为
项和为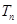 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和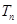 ;
;
(3)是否存在正整数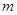 ,
, (
(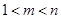 ),使得
),使得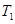 ,
, ,
,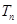 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的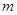 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R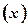 万元,且R
万元,且R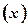

(1)写出年利润 关于年产量
关于年产量 的函数解析式;
的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
如图: PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当点E为BC的中点时,试判断EF与平面
PAC的位置关系,并说明理由;
(Ⅲ)证明:无论点E在边BC的何处,都有PE⊥AF.
已知函数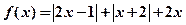 ,
,
 (Ⅰ)求函数
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 对任意
对任意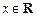 恒成立;命题
恒成立;命题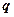 :指数函数
:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数
是增函数.若“p或q”为真,“p且q”为假,求实数 的取值范围.
的取值范围.
在直角坐标系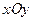 中,直线
中,直线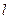 的参数方程为
的参数方程为 (
( 为参数),在极
为参数),在极
坐标系(与直角坐标系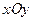 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为 。
。
①求圆C的直角坐标方程;
② 设圆C与直线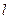 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为 ,求|PA|+|PB|。
,求|PA|+|PB|。
(本小题满分14分)
|
|
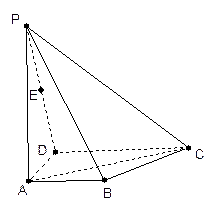
.如图,ABCD是梯形,AB//CD,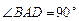 ,PA⊥面ABCD,
,PA⊥面ABCD,
|
(Ⅱ)求直线AC与PB所成角的余弦值;
(Ⅲ)在面PAB内能否找一点N,使NE⊥面PAC. 若存在,找出并证明;若不存在,请说明理由。