次体能测试中,规定每名运动员一开始就要参加且最多参加四次测试.一旦测试通过,就不再参加余下的测试,否则一直参加完四次测试为止.已知运动员甲的每次通过率为 (假定每次通过率相同)
(假定每次通过率相同)
(1) 求运动员甲参加测试的次数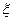 的分布列及数学期望;
的分布列及数学期望;
(2) 求运动员甲最多参加两次测试的概率(精确到 )
)
B.(选修4—2:矩阵与变换)
求使等式 成立的矩阵
成立的矩阵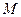 .
.
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4—1:几何证明选讲)
如图,在梯形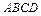 中,
中,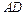 ∥BC,点
∥BC,点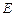 ,
,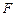 分别在边
分别在边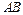 ,
, 上,设
上,设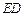 与
与 相交于点
相交于点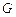 ,若
,若 ,
,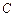 ,
,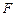 ,
,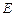 四点共圆,求证:
四点共圆,求证: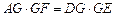 .
. 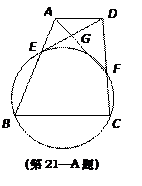
20.(本小题满分16分)
已知函数 .
.
(Ⅰ)若 有两个不同的解,求
有两个不同的解,求 的值;
的值;
(Ⅱ)若当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(Ⅲ)求 在
在 上的最大值.
上的最大值.
(本小题满分16分)已知椭圆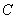 :
: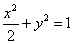 的左、右焦点分别为
的左、右焦点分别为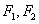 ,下顶点为
,下顶点为 ,点
,点 是椭圆上任一点,⊙
是椭圆上任一点,⊙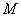 是以
是以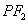 为直径的圆.
为直径的圆.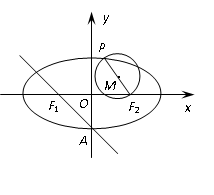
(Ⅰ)当⊙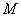 的面积为
的面积为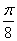 时,求
时,求 所在直线的方程;
所在直线的方程;
(Ⅱ)当⊙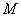 与直线
与直线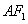 相切时,求⊙
相切时,求⊙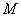 的方程;
的方程;
(Ⅲ)求证:⊙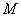 总与某个定圆相切.
总与某个定圆相切.
(本小题满分16分)
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示. 其上部分是以 为直径的半圆,点
为直径的半圆,点 为圆心,下部分是以
为圆心,下部分是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 是两根支杆,其中
是两根支杆,其中 米,
米, . 现在弧
. 现在弧 、线段
、线段 与线段
与线段 上装彩灯,在弧
上装彩灯,在弧 、弧
、弧 、线段
、线段 与线段
与线段 上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为
上装节能灯. 若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为 ,节能灯的比例系数为
,节能灯的比例系数为 ,假定该霓虹灯整体的“心悦效果”
,假定该霓虹灯整体的“心悦效果” 是所有灯“心悦效果”的和.
是所有灯“心悦效果”的和.
(Ⅰ)试将 表示为
表示为 的函数;
的函数;
(Ⅱ)试确定当 取何值时,该霓虹灯整体的“心悦效果”最佳?
取何值时,该霓虹灯整体的“心悦效果”最佳?