某市规定中学生百米成绩达标标准为不超过16秒.现从该市中学生中按照男、女生比例随机抽取了50人,其中有30人达标.将此样本的频率估计为总体的概率.
（1）随机调查45名学生,设ξ为达标人数,求ξ的数学期望与方差.
（2）如果男、女生采用相同的达标标准,男、女生达标情况如下表:
| |
男 |
女 |
总计 |
| 达标 |
a=24 |
b= [ |
|
| 不达标 |
c= |
d=12 |
|
| 总计 |
|
|
n=50 |
根据表中所给的数据,完成2×2列联表（注：请将答案填到答题卡上），并判断在犯错误的概率不超过0.01的前提下能否认为“体育达标与性别有关”?若有,你能否给出一个更合理的达标方案?
附：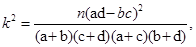
P（ ） |
0.025 |
0.01 |
0.005 |
0.001 |
 |
5.024 |
6.635 |
7.879 |
10.828 |
若函数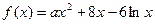
在点
处的切线方程为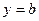
（1）求
的值；
（2）求
的单调递增区间；
（3）若对于任意的
，恒有
成立，求实数
的取值范围
将10个白小球中的3个染成红色，3个染成兰色，试解决下列问题：
（1）求取出3个小球中红球个数
的分布列和数学期望；
（2）求取
出3个小球中红球个数多于白球个数的概率
（本小题满分10分）选修4-5:不等式选讲
(Ⅰ)已知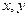
都是正实数，求证：
；
(Ⅱ)已知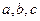
都是正实数，求证：
.
（本小题满分10分）选修4-4:坐标系与参数方程
在平面直角坐标系xOy中，已知曲线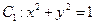
，将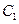
上的所有点的横坐标、纵坐标分别伸长为原来的
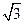、2倍后得到曲线
. 以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线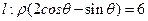
.
（Ⅰ）试写出直线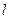
的直角坐标方程和曲线的参数方程；
（Ⅱ）在曲线上求一点P，使点P到直线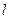的距离最大，并求出此最大值.
（本小题满分10分）选修4-1:几何证明选讲
如图所示，AB是⊙O的直径，
G为AB延长线上的一点，GCD是⊙O的割线，过点
G作AB的垂线，交AC的延长线于点E，交AD的延
长线于点F，过G作⊙O的切线，切点为H .
求证：（Ⅰ）C，D，F，E四点共圆；
（Ⅱ）GH2=GE·GF.