给定椭圆C: (a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ,求实数m的值.
,求实数m的值.
(本小题满分14分)
已知向量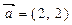 ,向量
,向量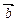 与
与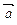 的夹角为
的夹角为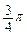 , 且
, 且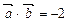 .
.
(1)求向量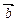 ;
;
(2)若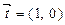 且
且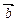
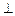
 ,
,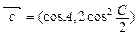 ,其中A、C是
,其中A、C是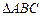 的内角,若三角形的三个内角A、B、C依次成等差数列,试求
的内角,若三角形的三个内角A、B、C依次成等差数列,试求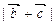 的取值范围
的取值范围
(本小题满分14分)
在锐角△ABC中,已知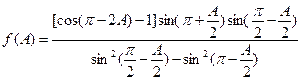 .
.
(1)求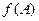 的最大值;
的最大值;
(2)当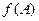 取得最大值时,
取得最大值时, ,如果
,如果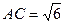 ,求
,求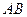 边和
边和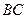 边的长.
边的长.
(本题15分)已知函数 是奇函数,且图像在点
是奇函数,且图像在点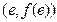
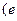 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.
(1)求实数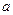 、
、 的值;
的值;
(2)若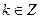 ,且
,且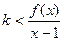 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值;
(3)当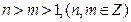 时,证明:
时,证明:
(本题15分)已知函数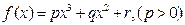 图象的对称中心为
图象的对称中心为 ,且
,且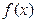 的极小值为
的极小值为 .
.
(1)求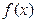 的解析式;
的解析式;
(2)设 ,若
,若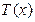 有三个零点,求实数
有三个零点,求实数 的取值范围;
的取值范围;
(3)是否存在实数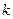 ,当
,当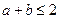 时,使函数
时,使函数
在定义域[a,b] 上的值域恰为[a,b],若存在,求出k的范围;若不存在,说明理由.
(本题14分)数列 的前
的前 项和为
项和为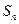 ,已知
,已知
(1)证明:数列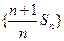 是等差数列,并求
是等差数列,并求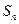 ;
;
(2)设 ,求证:
,求证: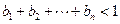 .
.