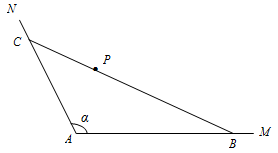
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.
命题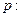 关于
关于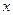 的不等式
的不等式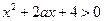 对一切
对一切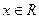 恒成立,
恒成立,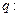 函
函
数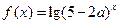 是增函数,若
是增函数,若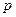 或
或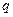 为真命题,
为真命题,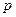 且
且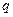 为假命题,求实数
为假命题,求实数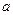 的取值范
的取值范
围。
已知函数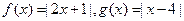 。(1)求不等式
。(1)求不等式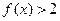 的解
的解
集;(2)若不等式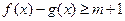 的解集为R,求实数m的取值范围。
的解集为R,求实数m的取值范围。
.设数列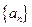 的前
的前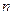 项和为
项和为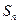 ,且
,且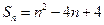 .
.
(1)求数列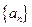 的通项公式;
的通项公式;
(2)设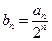 ,数列
,数列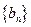 的前
的前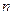 项和为
项和为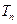 ,求证:
,求证: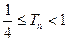 .
.
.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为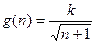 (k>0,k为常数,
(k>0,k为常数,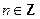 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为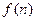 万元.
万元.
(1)求k 的值,并求出
的值,并求出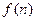 的表达式;
的表达式;
(2)问从今年算起第几年利润最高?最高利润为多少万元?
已知数列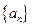 中,
中,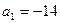 ,
,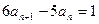 ,
,
(1) 证明:
证明: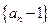 是等比数列;
是等比数列;
(2)若数列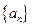 的前
的前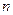 项和为
项和为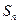 ,求数列
,求数列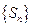 的通项公式,并求出n为何值时,
的通项公式,并求出n为何值时,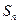 取得最小值,并说明理由。(参考数据:
取得最小值,并说明理由。(参考数据: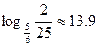 )
)