.设数列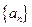 的前
的前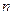 项和为
项和为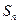 ,且
,且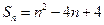 .
.
(1)求数列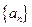 的通项公式;
的通项公式;
(2)设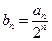 ,数列
,数列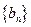 的前
的前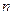 项和为
项和为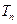 ,求证:
,求证: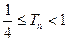 .
.
已知数列{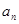 }的前n项和
}的前n项和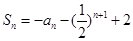 (n为正整数)。
(n为正整数)。
(1)令 ,求证数列{
,求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{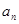 }的通项公式;
}的通项公式;
(2)令 ,
, ,求
,求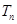 并证明:
并证明: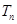 <3.
<3.
已知椭圆C: (a>b>0),过点(0,1),且离心率为
(a>b>0),过点(0,1),且离心率为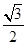 .
.
(1)求椭圆C的方程;
(2)A,B为椭圆C的左右顶点,直线l:x=2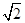 与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,
与x轴交于点D,点P是椭圆C上异于A,B的动点,直线AP,BP分别交直线l于E,F两点.证明:当点P在椭圆C上运动时,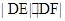 恒为定值.
恒为定值.
己知a∈R,函数
(1)若a=1,求曲线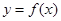 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;
(2)若|a|>1,求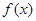 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.
如图①,已知 ABC是边长为l的等边三角形,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将
ABC是边长为l的等边三角形,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将 ABF沿AF折起,得到如图②所示的三棱锥A-BCF,其中BC=
ABF沿AF折起,得到如图②所示的三棱锥A-BCF,其中BC= .
.
(1)证明:DE//平面BCF;
(2)证明:CF 平面ABF;
平面ABF;
(3)当AD= 时,求三棱锥F-DEG的体积
时,求三棱锥F-DEG的体积
爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回.
(1)若爸爸恰好抽到了黑桃4.
①请把右面这种情况的树形图绘制完整;
②求亮亮抽出的牌的牌面数字比4大的概率.
(11)爸爸、亮亮约定,若爸爸抽到的牌的牌面数字比亮亮的大,则爸爸胜;反之,则亮亮赢,你认为这个游戏是否公平?如果公平,请说明理由,如果不公平,更换一张扑克牌使游戏公平.