已知函数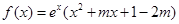 ,其中
,其中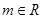 .
.
(Ⅰ)当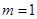 时,求函数
时,求函数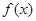 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:对任意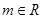 ,函数
,函数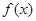 的图象在点
的图象在点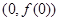 处的切线恒过定点;
处的切线恒过定点;
(Ⅲ)是否存在实数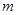 的值,使得函数
的值,使得函数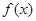 在
在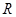 上存在最大值或最小值?若存在,求出实数
上存在最大值或最小值?若存在,求出实数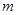 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
在△ABC中,A,B,C所对的边分别是
(1)用余弦定理证明:当C为钝角时, ;
;
(2)当钝角△ABC的三边 是三个连续整数时,求△ABC外接圆的半径.
是三个连续整数时,求△ABC外接圆的半径.
如图,已知 与圆
与圆 相切于点
相切于点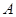 ,经过点
,经过点 的割线
的割线 交圆
交圆 于点
于点 、
、 ,∠APC的平分线分别交
,∠APC的平分线分别交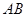 、
、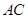 于点
于点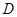 、
、 .
.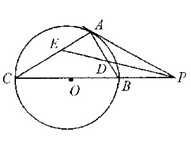
(1)证明:∠ADE=∠AED;
(2)若AC=AP,求 的值.
的值.
正方体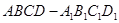 中,连接
中,连接 .
.
(1)求证: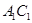 ∥平面
∥平面 ;
;
(2)求证:平面 ∥平面
∥平面 ;
;
(3)设正方体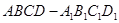 的棱长为
的棱长为 ,求四面体
,求四面体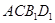 的体积.
的体积.
如图,四棱锥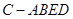 中,四边形
中,四边形 是正方形,若
是正方形,若 分别是线段
分别是线段 的中点.
的中点.
(1)求证: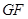 ||底面
||底面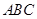 ;
;
(2)若点 为线段
为线段 的中点,平面
的中点,平面 与平面
与平面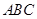 有怎样的位置关系?并证明。
有怎样的位置关系?并证明。
在 中,三内角
中,三内角 、
、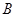 、
、 的对边分别是
的对边分别是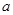 、
、 、
、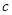 .
.
(1)若 求
求 ;
;
(2)若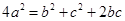 ,
,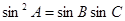 ,试判断
,试判断 的形状.
的形状.