如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.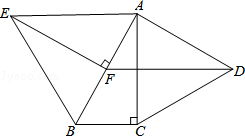
现在各地房产开发商,为了获取更大利益,缩短楼间距,以增加住宅楼栋数。合肥市某小区正在兴建的若干幢20层住宅楼,国家规定普通住宅层高宜为2.80米.如果楼间距过小,将影响其他住户的采光(如图所示,窗户高1.3米)。
(1)合肥的太阳高度角(即正午太阳光线与水平面的夹角):夏至日为81.4度,冬至日为34.88度。为了不影响各住户的采光,两栋住宅楼的楼间距至少为多少米?
(2)有关规定:平行布置住宅楼,其建筑间距应不小于南侧建筑高度的1.2倍;按照此规定,是否影响北侧住宅楼住户的全年的采光?若有影响,试求哪些楼层的住户受到影响?
(本题参考值:sin81.4º="0.99," cos81.4º="0.15," tan81.4º="6.61;" sin34.88º="0.57," cos34.88º="0.82," tan34.88º=0.70)
如图所示,一次函数y=k1x+b与反比例函数y= (x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式k1x+b> 的解.
的解.
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-l,-2和-3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定点Q的一个坐标为(a,b).
⑴用列表或画树状图的方法写出点Q的所有可能坐标;
⑵求点Q落在直线y=x-3上的概率.
如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.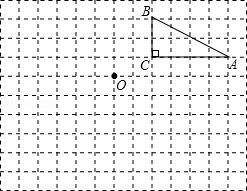
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2,请画出△A2B2C2.
(3)若点O的坐标为(0, 0),点B的坐标为(2, 3);写出△A1B1C1与△A2B2C2的对称中心的坐标
清明节前,某班分成甲、乙两组去距离学校4km的烈士陵园扫墓.甲组步行,乙组骑自行车,他们同时从学校出发,结果乙组比甲组早20min到达目的地.已知骑自行车的速度是步行速度的2倍,试求步行的速度.