如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.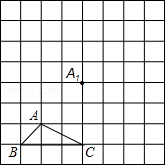
今年植树节,东方红中学组织师生开展植树造林活动,为了了解全校800名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
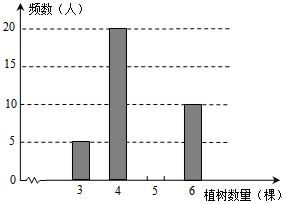
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校800名学生的植树数量.
一件外衣的进价为200元,按标价的8折销售时,利润率为10%,求这件外衣的标
价为多少元?(注: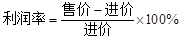 )
)
如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.求证:AD=CF.
解方程: .
.
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=﹣x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.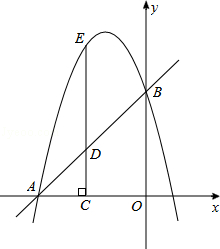
(1)求抛物线的解析式.
(2)当DE=4时,求四边形CAEB的面积.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求此点D坐标;若不存在,说明理由.