今年植树节,东方红中学组织师生开展植树造林活动,为了了解全校800名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
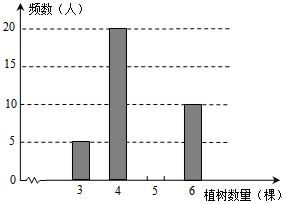
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校800名学生的植树数量.
如图,以 为直径的 外接于 ,过 点的切线 与 的延长线交于点 , 的平分线分别交 , 于点 , ,其中 , 的长是一元二次方程 的两个实数根.
(1)求证: ;
(2)在线段 上是否存在一点 ,使得四边形 是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.

如图,直线 , 都与双曲线 交于点 ,这两条直线分别与 轴交于 , 两点.
(1)求 与 之间的函数关系式;
(2)直接写出当 时,不等式 的解集;
(3)若点 在 轴上,连接 把 的面积分成 两部分,求此时点 的坐标.

“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了八年级50名学生最近一周的读书时间,统计数据如下表:
|
时间(小时) |
6 |
7 |
8 |
9 |
10 |
|
人数 |
5 |
8 |
12 |
15 |
10 |
(1)写出这50名学生读书时间的众数、中位数、平均数;
(2)根据上述表格补全下面的条形统计图.
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于9小时的概率是多少?

已知:如图, 是任意一个三角形,求证: .

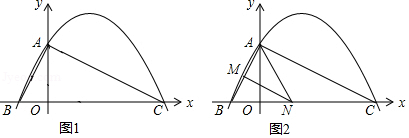
如图1,已知二次函数 的图象与 轴交于点 ,与 轴交于点 、 ,点 坐标为 ,连接 、 .
(1)请直接写出二次函数 的表达式;
(2)判断 的形状,并说明理由;
(3)若点 在 轴上运动,当以点 、 、 为顶点的三角形是等腰三角形时,请写出此时点 的坐标;
(4)如图2,若点 在线段 上运动(不与点 、 重合),过点 作 ,交 于点 ,当 面积最大时,求此时点 的坐标.