我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。如图1，四边形ABCD即为“准等腰梯形”。其中∠B=∠C．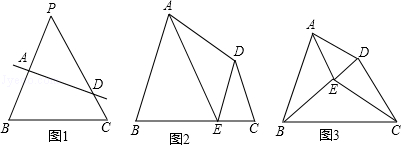
（1）在图1所示的“准等腰梯形”ABCD中，选择合适的一个顶点引一条直线将四边形ABCD分割成一个等腰梯形和一个三角形或分割成一个等腰三角形和一个梯形（画出一种示意图即可）；
（2）如图2，在“准等腰梯形”ABCD中∠B=∠C．E为边BC上一点，若AB∥DE，AE∥DC，求证：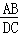
=
；
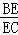（3）在由不平行于BC的直线AD截△PBC所得的四边形ABCD中，∠BAD与∠ADC的平分线交于点E。若EB=EC，请问当点E在四边形ABCD内部时（即图3所示情形），四边形ABCD是不是“准等腰梯形”，为什么？若点E不在四边形ABCD内部时，情况又将如何？写出你的结论。（不必说明理由）
解下列方程（每小题4分，共16分）.
（1）
；
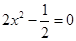（2）
(配方法) ；
（3）
；
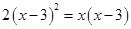（4）
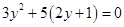(公式法) ．
随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润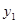
与投资量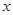
成正比例关系，如图（1）所示；种植花卉的利润
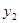与投资量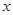成二次函数关系，如图（2）所示（注：利润与投资量的单位：万元）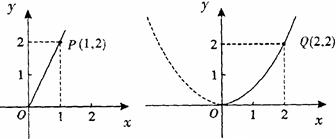
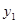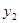（1）分别求出利润与关于投资量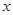的函数关系式；
（2）如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？
如图，⊙O与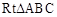
的斜边AB相切于点D，与直角边AC相交于E、F两点，连结DE，已知
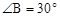，⊙O的半径为12，弧DE的长度为
．
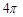（1）求证：DE∥BC；
（2）若AF=CE，求线段BC的长度．
完全相同的4个小球，上面分别标有数字1、－1、2、－2，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次．把第一次、第二次摸到的球上标有的数字分别记作m、n，以m、n分别作为一个点的横坐标与纵坐标，
（1）若第一次摸出球后放回摇匀，求点（m，n）不在第二象限的概率．（用列表法求解）
（2）若第一次摸出球后不放回，求点（m，n）不在第二象限的概率．（用树状图求解）
在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C =90°，AC=3，BC=4．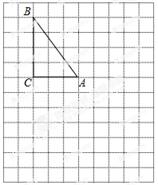
（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；
（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并标出A、C两点的坐标；
（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并标出B2、C2两点的坐标．