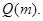已知圆 过定点
过定点 ,圆心
,圆心 在抛物线
在抛物线 上,
上, 、
、 为圆
为圆 与
与 轴的交点.
轴的交点.
(Ⅰ)当圆心 是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
是抛物线的顶点时,求抛物线准线被该圆截得的弦长.
(Ⅱ)当圆心 在抛物线上运动时,
在抛物线上运动时, 是否为一定值?请证明你的结论.
是否为一定值?请证明你的结论.
(Ⅲ)当圆心 在抛物线上运动时,记
在抛物线上运动时,记 ,
, ,求
,求 的最大值,并求出此时圆
的最大值,并求出此时圆 的方程.
的方程.
已知:曲线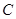 上任意一点到点
上任意一点到点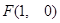 的距离与到直线
的距离与到直线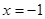 的距离相等.
的距离相等.
(1)求曲线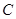 的方程;
的方程;
(2)如果直线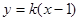 交曲线
交曲线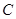 于
于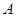 、
、 两点,是否存在实数
两点,是否存在实数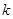 ,使得以
,使得以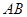 为直径的圆经过原点
为直径的圆经过原点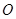 ?若存在,求出
?若存在,求出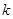 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知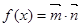 ,其中
,其中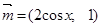 ,
,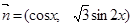
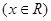 .
.
(1)求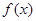 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)在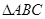 中,
中,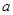 、
、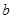 、
、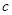 分别是角
分别是角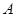 、
、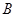 、
、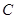 的对边,若
的对边,若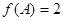 ,
,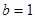 ,
,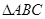 面积为
面积为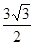 ,求:边
,求:边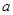 的长及
的长及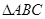 的外接圆半径
的外接圆半径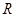 .
.
在长方体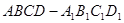 中,
中,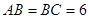 ,用过
,用过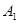 ,
,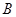 ,
,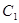 三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
(1)求棱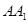 的长;
的长;
(2)求点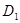 到平面
到平面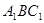 的距离.
的距离.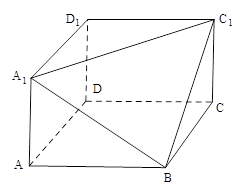
设函数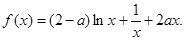
(1)当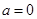 时,求
时,求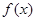 的极值;
的极值;
(2)当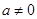 时,求
时,求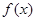 的单调区间;
的单调区间;
(3)当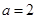 时,对任意的正整数
时,对任意的正整数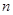 ,在区间
,在区间 上总有
上总有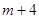 个数使得
个数使得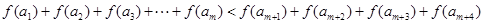 成立,试求正整数
成立,试求正整数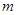 的最大值。
的最大值。
(本小题满分12分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交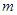 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为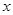 元(
元(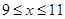 )时,一年的销售量为
)时,一年的销售量为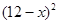 万件.
万件.
(1)求分公司一年的利润L(万元)与每件产品的售价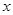 (元)的函数关系式;
(元)的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出L的最大值