“太空粒子探测器”是由加速、偏转和收集三部分组成,其原理可简化如下:如图甲所示,辐射状的加速电场区域边界为两个同心平行半圆弧面,圆心为O,外圆弧面AB的半径为L,电势为φ1,内圆弧面CD的半径为L/2,电势为φ2。足够长的收集板MN平行边界ACDB,O到MN板的距离OP为L。假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到AB圆弧面上,并被加速电场从静止开始加速,不计粒子间的相互作用和其它星球对粒子引力的影响。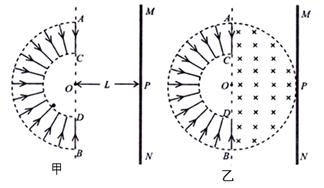
(1)求粒子到达O点时速度的大小:
(2)如图乙所示,在边界ACDB和收集板MN之间加一个半圆形匀强磁场,圆心为O,半径为L磁场方向垂直纸面向内,则发现从AB圆弧面收集到的粒子有2/3能打到MN板上(不考虑过边界ACDB的粒子再次返回),求所加磁感应强度的大小;
(3)随着所加磁场大小的变化,试定量分析收集板MN上的收集效率η与磁感应强度B的关系。
如图所示,三根轻线结于O点,并分别与套环A、B和重物C连接,A、B环重均为50N,套在水平横杆上,C重为120N,AO与BO两线等长并与横杆的夹角均为37°,整个系统处于静止状态,(sin37°=0.6,cos37°=0.8)求:
AO与BO两线中的张力大小;
A环所受杆的弹力与摩擦力的大小;
若将B点向左移一点后系统仍处于静止状态,与原来相比,A环所受线的拉力、杆的支持力和摩擦力大小分别如何变化?
有甲、乙两运动员做接棒练习,甲在接力区前s0=18m处作了标记,并以v1=8.5m/s的恒定速度跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令的同时起跑,并做匀加速运动,在速度达到v2=8m/s时被甲追上,完成交接棒。求:此次练习中乙在接棒前的加速度a。
已知接力区的长度为L=20m,在完成交接棒时乙离接力区末端的距离s。
如图所示,在竖直向下,场强为E的匀强电场中,长为l的绝缘轻杆可绕固定轴O在竖直面内无摩擦转动,两个小球A、B固定于杆的两端,A、B的质量分别为m1和m2(m1<m2),A带负电,电量为q1,B带正电,电量为q2。杆从静止开始由水平位置转到竖直位置,求: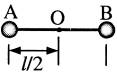
在此过程中电场力所做的功为多少?
在竖直位置处两球的总动能为多少?
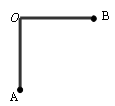
若将轻杆弯折成如图所示的“Γ”形,两边互相垂直、长度均为l/2 ,两端各固定一个金属小球A、B,在竖直向下,场强为E的匀强电场中,可绕过O点的水平轴在竖直平面内无摩擦转动。已知A球质量m1=m,电量为+q,B球质量m2=7m/2,B球也带负电,电量为-q。现将“Γ”形杆从OB位于水平位置由静止释放,求:OB杆能转过的最大角度为127°,则该电场强度的大小为多少?
当两球的速度达到最大时,OB杆转过的角度为多大?
如图甲所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨,在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,其磁感应强度随时间变化的规律如图乙所示。在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.2Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响。求: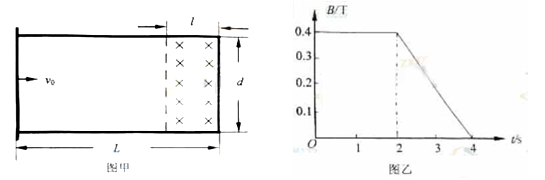
导体棒从t=0时刻开始向右运动直至末速为零所需的时间;
导体棒从t=0时刻开始向右运动直至末速为零时离左端的位置;
4s内回路中电流的大小,并判断电流方向;
4s内回路产生的焦耳热。
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3的初速度由A点开始向B点滑行,AB=5R,并滑上光滑的半径为R的1/4圆弧BC,在C点正上方有一离C点高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,旋转时两孔均能达到C点的正上方。 求:
滑块刚到B 处的速度;
滑块滑过C点,穿过小孔P时的速度;
若滑块穿过后P孔后,又恰能从Q孔落下,则平台转动的角速度ω应满足什么条件?